
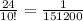

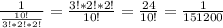
1. Упростите выражение (2b + a) · (a - 2b) - (2b + a)² и найдите его значение, если a = -0,5 , b = 2.
(2b + a) · (a - 2b) - (2b + a)² = (a + 2b) · (a - 2b) - (4b² + 4ab + a²) = a² - 4b² - 4b² - 4ab - a² = - 8b² - 4ab ; a = -0,5 , b = 2 ⇒ - 8 · 2² - 4 · (-0,5) · 2 = - 8 · 4 + 2 · 2 = - 32 + 4 = - 28.
2. Докажите, что для любого n значение выражения (3n + 1)² - (3n - 1)² кратно числу 12.
(3n + 1)² - (3n - 1)² = ( 3n + 1 - (3n - 1) ) · (3n + 1 + 3n - 1) = 2 · 6n = 12n.
Так как результат умножения любого числа на 12 кратен 12, то значение выражения 12n кратно 12 при любых значениях переменной n, что и требовалось доказать.
(х + у)^2 -70 = х^2 + y^2
x^2 + 2xy +y^2 - 70 = x^2 + y^2
2xy = 70
xy = 35 (второе уравнение)
из первого выражаем переменную , получаем подстановку х = 12 - у и подставляем во второе
имеем y^2 -12у + 35 = 0.
D = 144 -4*35 = 4
у = 7; х = 5 (первая пара)
у = 5; х = 7 (вторая пара)
. ответ: (5;7); (7;5)