Відповідь:
Еще недавно, учась сложению чисел, мы складывали кучки из монет. Тогда перед нами стояла задачи сложить две кучки. Но допустим, мы хотим теперь сложить не две, а несколько кучек. Это можно было бы сделать так: сгребаем их все сразу в одну большую кучу и пересчитываем в ней все монеты. Такой сложения всем бы был хорош, да только ни на счетах, ни на бумаге нельзя сделать ничего подобного. На счетах и бумаге мы умеем складывать между собой только два числа. Поэтому мы не будем сгребать вместе сразу все кучки, а поступим так, чтобы все наши действия можно было легко перенести на бумагу.
Итак, перед нами несколько кучек из монет. Мы знаем, сколько монет в каждой кучке, и теперь мы хотим узнать, сколько же у нас всего монет во всех кучках. Мы берем любые две кучки и сдвигаем их вместе, образуя одну новую кучку побольше. Умея складывать два числа на бумаге, мы сможем легко вычислить, сколько у нас монет в новой кучке без фактического их пересчета. Теперь у нас стало на одну кучку меньше. Далее, берем еще две кучки, сливаем их воедино, вычисляем новое число монет в только что образованной кучке и, таким образом, снова уменьшаем количество кучек на одну. Мы повторяем и повторяем эту процедуру, уменьшая всякий раз число кучек на единицу, до тех пор пока у нас не останется одна-единственная большая куча. Число монет в этой куче нам известно, причем вычислили мы его на бумаге, а не прямым пересчетом.
Очевидно, мы получим один и тот же ответ, совершенно независимо от того, в каком порядке мы сдвигали кучки. А значит, когда перед нами находится сумма чисел, например,
8 + 9 + 2, мы можем вычислять ее тоже в любом порядке. Поэтому мы всегда будем выбирать такой порядок, какой для нас наиболее удобен. В данном случае удобно вначале сложить восьмерку и двойку, а потом добавить девятку:
8 + 2 + 9 = 10 + 9 = 19.
1) D(y) = [0; + ∞) \ {1; 2/3}
2) D(y) = [–3; 3] \ {–2}.
Объяснение:
Области определения тут могут быть ограничены следующим: определением корня чётной степени, а также тем, что знаменатель в дроби не равен нулю.
1) Присутствует
![\sqrt[4]{x}](/tpl/images/1100/2819/19eed.png)
Значит х≥0.
Далее знаменатель ≠ 0. Кстати, это ещё и корень с чётной степенью (2), т.е. есть ещё и ограничение, что
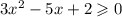
А когда корень из числа равен нулю? Тогда и только тогда, когда само подкоренное выражение равно нулю. И да, всё решение рассматриваем на множестве действительных (они же вещественные) чисел.
Значит нужно решить квадратное уравнение, тогда его корни и будут недопустимыми значениями.
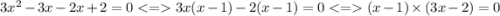
Т. о. получается совокупность – либо х = 1, либо 3х = 2. Значит либо х = 1, либо х = 2/3. Так как оба корня является решением квадратного уравнения, при них выражение не будет определено (деление на ноль) т.е. в область определения следует записать: х ≠ 1, х≠2/3.
Т.о. следующие ограничения: х≥0, х ≠ 2/3, х≠1. Все они должны выполняться одновременно, значит D(y) = [0; + ∞) \ {1; 2/3}. Если что, D – обозначение области определения функции, \ – операция "вычитания" из множества.
2) Тут знаменатель тоже не должен быть равен нулю т.е. х + 2 ≠ 0 <=> х ≠ –2.
И также в числителе корень с чётной степенью, значит подкоренное выражение
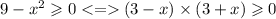
Предлагаю решить методом интервалов, так как здесь сравнение с нулём.
Необходимо начертить координатную ось с соответствующей подписью (в данном случае х), далее отметить значения, при которых один из множителей обращается в ноль – здесь это х = 3 и х = – 3. Так получились три области, в которых значение произведения/выражения данного одного знака (больше или меньше нуля) Далее подставляем в х огроооомное число, явно превышающее 3 (обозначенное число-граница) т.к. так удобнее и узнаём, больше или меньше 0 это произведение – оно меньше, значит ставим минус в той области. Далее можно не подставлять, а понять, что так как нет других множителей и множителя в чётной степени, знак выражения в областях будет чередоваться. Числа-границы нужно учитывать в ответ (закрашивая), если выражение может быть равно нулю (т.е. ≥0) Таким образом решением является следующее множество: [–3; 3]
Все условия/ограничения должны выполняться, т.е. получается система из х≠–2 и 3 ≥ х ≥–3. Значит область определения D(y) = [–3; 3] \ {–2}.


= 36x² + x⁴ + 18x - x⁴ + x² = 37x² + 18x = x( 37x + 18)