
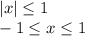
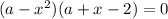

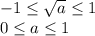
![a \in [0;1]](/tpl/images/0775/0492/4bfc3.png) - неравенства будут иметь общее решение, значит при
- неравенства будут иметь общее решение, значит при 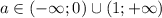 неравенства общих решений не будет иметь
неравенства общих решений не будет иметь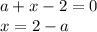
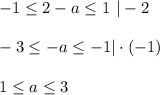
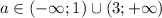 неравенства общих решений не имеют
неравенства общих решений не имеют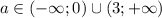
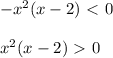
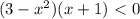
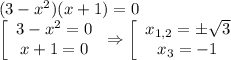
![a \in (-\infty;0]\cup[3;+\infty)](/tpl/images/0775/0492/a3d1e.png)
19320
Объяснение:
Обозначим сумму
S=40+41+42+...+198+199+200.
Вычислим сумму двумя Отметим, что в сумме количество слагаемых равен (200-40)+1=161.
Выражения для суммы напишем двумя и суммируем почленно:
S= 40 + 41 + 42 +...+198+199+200
S=200+199+198+...+ 42 + 41 + 40
Тогда:
2·S=(40+200)+(41+199)+(42+198)+...+(198+42)+(199+41)+(200+40)=
=240+240+240+...+240+240+240=161·240=38640.
Отсюда
S=38640:2=19320.
Можем рассмотреть сумму как сумма членов арифметической прогрессии с первым членом a₁=40 и d=1. Применим формулу для суммы первых n-членов арифметической прогрессии:
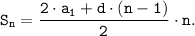
Так как n=161, то
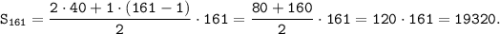
sinx-sin5x=cos5x-cosx
2*sin(x-5x)/2*cos(x+5x)/2=-2*sin(5x-x)/2*sin(5x+x)/2
-2*sin2x*cos3x=-2*sin2x*sin3x
-2*sin2x*cos3x+2*sin2x*sin3x=0
2*sin2x*(sin3x-cos3x)=0
Произведение равно нулю, когда один из множителей равен нулю.
1) sin2x=0 <=> 2x=pi*m <=> x=pi*m*2
В этой серии наибольший отрицательный корень будет при m=-1: x=-pi/2
2) sin3x-cos3x=0
Т.к. по формулам приведения cos3x=sin(pi/2-3x), то получим:
sin3x-sin(pi/2-3x)=0
2*sin(3x-pi/2+3x)/2*cos(3x+pi/2-3x)/2=0}br> 2*sin(3x-pi/4)*cos(pi/4)=0
Сокращаем константы:
sin(3x-pi/4)=0
3x-pi/4=pi*n
x=pi/12+pi*n/3
В это серии имеем, что при n=0 корень ещё положительный: x=pi/12, а при n=-1 получаем х=pi/12-pi/3=-3*pi/12=-pi/4. Т.к. -pi/4>-pi/2, то этот корень и будет наибольшим отрицательным.
ответ: -pi/4.