Решить примеры неполные кв.уравнения (^ таким значком буду означать квадраты) 13-х^2=0 x^2-14=0 x^2-15=0 - id498868420210601 от Kseniya204 01.06.2021 23:36

Question

Алгебра: Решить примеры неполные кв.уравнения (^ таким значком буду означать квадраты) 13-х^2=0 x^2-14=0 x^2-15=0 x^2+4=0 64-x^2=0 12x^2=0 4x^2=0 -x^2=0 -x^2-10x=0 -x^2-5x=0 x^2+6x=0 x^2-11x=0 12x-x^2=0 вот пож.щас карантин тему прочла ,но примеры не все поняла как решать для примера решите эти . вам огромное заранее*

Kseniya204 · Accepted Answer

Область определения - это множество всех таких значений аргумента х, при которых функция определена, Т.е. выражение, которым задается функция при всех таких х имеет смысл.
Например, функция y= 5x - 1

совершенно очевидно , что выражение 5x - 1   имеет смысл при любых значениях х, поэтому у неё область определения - это множество всех действительных чисел: D(f) = R.
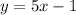
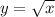
Функция $y = \sqrt{x} \\$
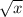т.к. выражение $\sqrt{x}$ имеет смысл   только при х≥0, то
область определения этой функции - это множество всех неотрицательных чисел: D(f) = [ 0; + oo )

Множество значений функции - это просто множество всех значений, которые принимает данная функция.
   y= 5x - 1

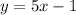Множество значений - все действительные числа:
Е(f) = R
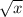$\sqrt{x}$ Множество значений - это также множество всех неотрицательных чисел: Е(f) = [ 0; + oo )

MOGZ ответил