2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
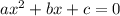
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
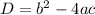
Формула корней:
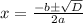
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
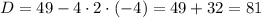
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
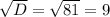
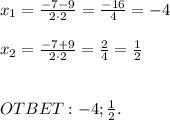
1)В таблице.
2)Не проходит.
Объяснение:
1) Построить график функции у=2х-2.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -4 -2 0
2) Определить, проходит ли график функции через точку А(-10; -20).
Для этого нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть равна правой, то проходит, и наоборот:
у=2х-2
-20=2*(-10)-2
-20≠ -22, не проходит.
y+20y=1,05
21y=1,05
y=0,05
20^(x+4)=20^(-1)
x=5