Объяснение:
Решение методом интервалов
(x-5) (3-7x) (2x+8)≤0
найдем корни
х-5=0 ; x₁=5
3-7x=0 ; x₂=3/7
2x+8=0 ; x₃=-4
нанесем корни на числовую ось в порядке возрастания, определим знак выражения (x-5)(3-7x)(2x+8) на каждом интервале, для этого берем число из каждого интервала подставляем его в (x-5)(3-7x)(2x+8) и определяем знак
(-∞)[-4][3/7][5](+∞)>
(-5-5)(3-7*(-5))(-10+8)>0 знак (+)
(0-5)(3-7*0)(2*0+8)>0 знак (-)
(3-5)(3-7*3)(2*3+8)>0 знак (+)
(6-5)(3-7*6)(2*6+8)>0 знак (-)
(-∞)[-4][3/7][5](+∞)>
+ - + -
Выбираем интервалы со знаком (-)
x∈[-4;3/7]U[5;+∞)
В решении.
Объяснение:
а) Дана функция у = х³.
График - кубическая парабола.
Область определения - это проекция графика функции на ось Ох.
Обозначается как D(f) или D(у).
Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
Обычно запись: D(у) = R.
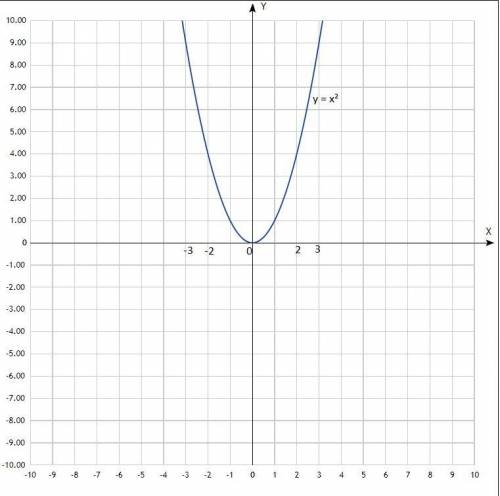
б) Дана функция у = х².
График - классическая парабола с вершиной в начале координат (0; 0).
Построить график.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
По вычисленным точкам построить параболу.
Промежуток возрастания функции: х∈(0; +∞).
25x²-30x+9+144x²+120x+25≤49-182x+169x²+34x²+17x+410
34x²-255x+425≥0
D=7225
x=255+85/68=5
x=255-85/68=2,5
a=34 больше 0, ветви вверх.
(-бескон;2,5)и (5;;+бесконечн)