варианта 2 как можно понимать эти выражения (запись в условии немного запутывает):
1.
2.
то есть роли не играет, потому что выражение имеет вид
сначала прибавляем выражение, а потом его вычитаем, ну а единица тут спокойно прибавляется и она в ответе.
upd. оказывается, что выражение, по всей видимости, такое:
если это так, то в условии, конечно, лучше ставить скобки
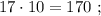
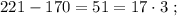
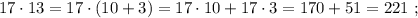
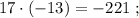
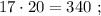
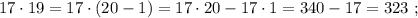
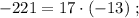
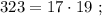
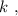каждое из которых представляет собой какое-то допустимое нечётное число, умноженное на 17, тогда можно сложить все эти допустимые нечётные числа и умножить их на 17 (вынести за скобку общий множитель).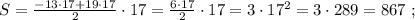
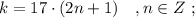
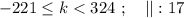
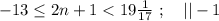
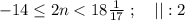
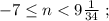
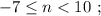
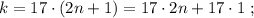
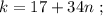
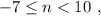который пробегает 
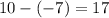разных значений.![S = \frac{ [ 17 + 34 \cdot (-7) ] + [ 17 + 34 \cdot 9 ] }{2} \cdot 17 = \frac{ 2 \cdot 17 + 34 \cdot ( -7 + 9 ) }{2} \cdot 17 = \\\\ = ( 17 + \frac{ 34 \cdot 2 }{2} ) \cdot 17 = ( 17 + 17 \cdot 2 ) \cdot 17 = 17^2 \cdot 3 = 289 \cdot 3 = 867 \ ;](/tpl/images/0532/7209/6e09f.png)
x^3/3-2x^2/2+3x
Далее используешь формулу Ньютона-Лейбница.
((-1)^3/3-2/2-3)-(2^3/3-2*2^2+3^2)=(-1-1-3)-(8/3-8+9)=-5-(8/3+1)=-5-(11/3)=-5-11/3=-26/3