Решаем полное квадратное уравнение x^2 - 5x + 6 = 0 с нахождения дискриминанта.
Вспомним формулу для нахождения дискриминанта:
D = b^2 - 4ac;
Найдем дискриминант для заданного уравнения.
D = (-5)^2 - 4 * 1 * 6 = 25 - 24 = 1;
Дискриминант найден перейдем к нахождению корней.
x1 = (-b + √D)/2a = (5 + √1)/2 * 1 = (5 + 1)/2 = 6/2 = 3;
x2 = (-b - √D)/2a = (5 - √1)/2 * 1 = (5 - 1)/2 = 4/2 = 2;
Корни найдены. Сделаем проверку:
1) 3^2 - 5 * 3 + 6 = 0;
9 - 15 + 6 = 0;
0 = 0;
2) 2^2 - 5 * 2 + 6 = 0;
4 - 10 + 6 = 0;
0 = 0.
а) 2x^2-11x+12=0
2x^2-3x-8x+12=0
(2x-3)*(x-4)=0
2x-3=0 или x-4=0
2x=0+3 x=4
2x=3
x=3:2
x=1,5
б) 14x^2=9x
14x^2-9x=0
x(14x-9)=0
x=0 или 14x-9=0
x=9/14
в) 16x^2-49=0
16x^2=49
x^2=49:16
x^2=49/16
x=±7/4
г) x^2-36x+323=0
x(x-17)-19(x-17)=0
(x-17)(x-19)=0
x-17=0 или x-19=0
x=17 x=19
2.
p=46=2(a+b) все это делим на 2 чтобы от нее избавиться
23=a+b
b=23-a
s=120=ab
120=a(23-a)
120=23a-a^2
-a^2+23a-120=0
d=23^2-480=529-480=49
x1=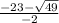 = -23-7/-2=-30/-2=15
= -23-7/-2=-30/-2=15
x2=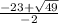 =-23+7/-2=-16/-2=8
=-23+7/-2=-16/-2=8
3.x^2+px=36=0 (a=1; b=p; c=36)
d=p^2-144
12=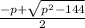
p=-15
x2=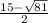 =15-9/2=6/2=3
=15-9/2=6/2=3