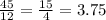
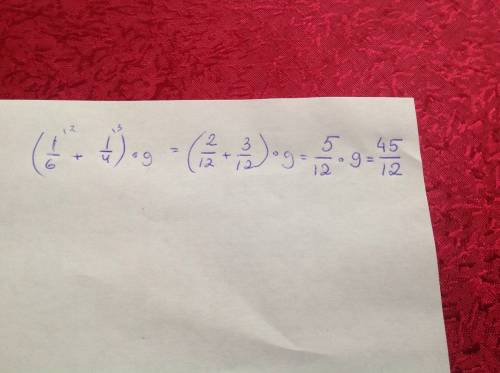
Домножив на y⁴, получаем
2*x*y dy + (y² - 3*x²) dx
2*x*y dy = (3*x² - y²) dx
dy / dx = (3*x² - y²)/(2*x*y) = 1,5*x/y - 0,5*y/x
При одновременном умножении х и у на одно и то же число правая часть не меняется, поэтому это однородное уравнение.
Пусть у = u * x . Тогда dy / dx = u + x * du / dx и уравнение принимает вид
u + x * du / dx = 1,5 / u - 0,5 * u
x * du / dx = 1,5 (u - 1 / u)
u du / (u² - 1) = 1,5 dx / x
1/2 ln (u² - 1) = 3/2 * ln x + 1/2 * ln C
(u² - 1) = C * x³
y² - x² = C * x⁵
y² = C * x⁵ + x²
Если при х = 1 у = 1, то С = 0 и решение уравнения у = х.
Тогда соответственно при х = 5 у = 5.
Нарисуем график функции Y = √ X как повернутую на 90 градусов левую половину параболы Y = X².
1) Проведем горизонтальную прямую Y = 3. Она пересекает данный график при Х = 9
2) Проведем горизонтальную прямую Y = 5. Она пересекает данный график при Х= 25
3) Проведем прямую Y = X (биссектрису прямого угла). Она пересекает график при Х = 0 и Х = 1. Следовательно, уравнение имеет 2 корня.
4) Поскольку функция корня определена при Х ≥ 0, то -Х ≤ 0 и, следовательно решением может быть только Х = 0. Это значение и будет единственным корнем.