х= -5
у=10 решение системы уравнений
Объяснение:
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, коэффициенты или при х, или при у должны быть одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают одно из уравнений, как бы подгоняют ко второму, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе уже есть одинаковые коэффициенты при у, ничего сильно преобразовывать не нужно, но знаки не противоположные, поэтому нужно какое-то из уравнений умножить на -1, например, первое:
-3х -2у= -5
-5х+2у=45
Сейчас просто складываем, следим за знаками:
-3х + (-5х)-2у+у = -5+45 приводим подобные члены:
-8х=40
х= -5
Теперь найденное значение х подставляем в любое из двух данных уравнений и вычисляем у:
-3*(-5) -2у= -5
15-2у= -5
-2у= -5 -15
-2у= -20
у=10
х= -5
у=10 решение системы уравнений
Для проверки можно подставить значения х и у в оба уравнения, правая и левая часть уравнений должны быть равны.
В данном примере равны, значит, решение верное.
1. Обратно пропорциональная зависимость :
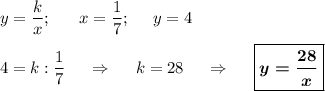
2. Решите графически 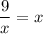
График функции 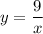 - гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
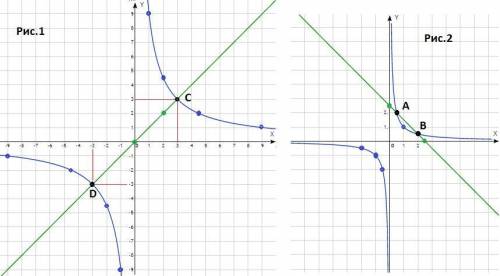
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции 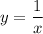 - гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.