
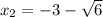
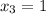

Объяснение:
(x² + 6x)² - 4(x² + 6x + 1) - 17 = 0
t = (x² + 6x)
t² - 4(t + 1) - 17 = 0
t² - 4t - 4 - 17 = 0
t² - 4t - 21 = 0
t² + 3t - 7t - 4 - 17 = 0 (Теорема Виета)
t² + 3t - 7t - 21 = 0
t(t + 3) - 7(t + 3) = 0
(t + 3)(t - 7) = 0
t₁ = -3; t₂ = 7
x² + 6x + 3= 0 x² + 6x - 7 = 0
D = b² - 4ac D = b² - 4ac
D = 6² - 4 * 1 * 3 D = 6² - 4 * 1 * (-7)
D = 36 - 12 D = 36 + 28
D = 24 D = 64
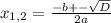



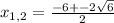

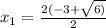

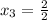
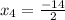

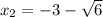
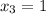

х(5+2х)=0
х=0
5+2х=0
2х=-5
х=-5/2
5+2х²=0
2х²=-5 х²=-5/2 х=√-5/2 решения нет,так как выражение под корнем квадратным не может быть отрицательным
5 - 2х² =0
2х²=5 х²=5/2 х=+/-√5/2 х1=√5/2 х2=-√5/2
2х² + (а-1)х=0
х(2х + (а-1))=0
х=0
2х+(а-1)=0
2х=-(а-1)
х=-(а-1)/2
ответ: х1=0
х2=-(а-1)/2