Решение системы уравнений х=2
у= -1
Объяснение:
Решить систему методом алгебраического сложения
3х+6у=0
2х-у-5=0
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно второе уравнение умножить на 6:
3х+6у=0
12х-6у=30
Складываем уравнения:
3х+12х+6у-6у=30
15х=30
х=30/15
х=2
Теперь значение х подставляем в любое из двух уравнений системы и вычисляем у:
3х+6у=0
6у= -3х
6у= -3*2
6у= -6
у= -1
Решение системы уравнений х=2
у= -1
8
Объяснение:
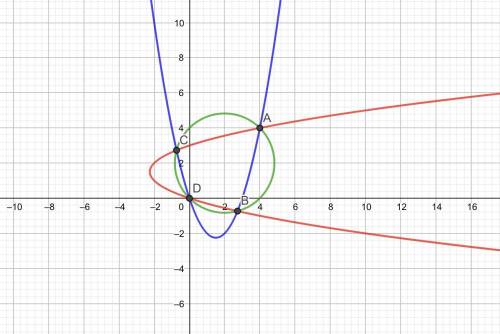
Складывая данные уравнения , получим : x² +y² = 4(x+y) ( 1 )
пусть x + y = a ⇒ y = a-x , подставим в ( 1 ) вместо y ( a -x ) :
x² +( a-x)² - 4a = 0 или : 2x² -2ax +a²-4a = 0 ( 2 )
уравнение (2) имеет решение , если D/4 ≥ 0 или :
a² -2(a² -4a) ≥ 0 ⇔ a² -8a ≤ 0 ⇔ 0 ≤ a ≤ 8 ⇒ наибольшее a , при
котором уравнение ( 2 ) имеет решение равно 8 ⇒ a ≤ 8 ;
проверкой убеждаемся , что пара ( 4 ; 4) является решением
системы и мы доказали , что x+y ≤ 8 ⇒ 8 - наибольшее
значение суммы (x+y)
4x²+12x-x-3=x²-4x-3
3x²+15x=0
x*(3x+15)=0
(-5+0):2=-2,5