Р пр-ка = 60 м
Sдор. = 64 м²
шир. дор. = ? м
Решение.
Если а и b - длина и ширина, соответственно, м, то
Рпр-ка = 2а + 2b ---- периметр здания
х, м ---- ширина дорожки
Площадь дорожки складывается из 8 участков, Двух равных по длине длине здания, двух равных по длине ширине здания и четырех квадратов по углам, со стороной равной стороне дорожки.
Sдор. = 4х² + 2ах + 2bх = 4х² + х(2а + 2b) = 4х² + х*Рпр-ка
4х² + 60х = 64 ----- по условию | : 4
х² + 15х - 16 = 0
D = 15² + 4*16 = 225 + 64 = 289 = 17²
х₁ =(-15 + √17²)/2 = (-15+17)/2 = 1 (м) ----- ширина дорожки
х₂ = (-15 - 17)/2 = - 16 м -- отбрасываем, как посторонний корень, не имеющий физического смысла
ответ: 1 м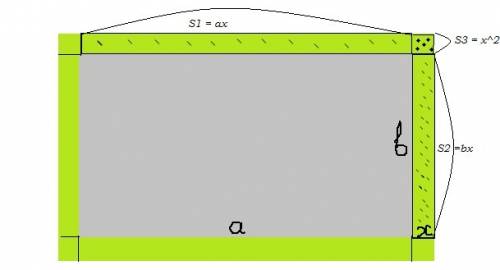
Объяснение:
а) 9x-3y=6;
Выражаем у через х и получаем линейную функцию:
3у=9х-6;
у=(9х-6)/3=3х-2;
у=3х-2.
Графиком линейной функции является прямая, прямую можно построить по двум точкам, например:
х у
0 -2
2 4
См. рисунок а).
б) y=-4x+2;
График линейной функции - прямая, строим ее по двум точкам, например:
х у
0 2
1 -2
См. рисунок б).
в) y=⅓x;
График прямой пропорциональности - это прямая, которая проходит через начало координат точку О(0;0).
Строим по двум точкам, например:
х у
0 0
3 1
См. рисунок в).
г) y=-x;
График прямой пропорциональности - прямая, которая проходит через начало координат точку О(0;0).
Строим по двум точкам, например:
х у
0 0
2 -2
См. рисунок г).
д) y=-5;
Графиком является прямая, которая проходит через точку (0;-5) и параллельно оси абсцисс (ОХ).
См. рисунок д).
e) x=4;
Графиком является прямая, которая проходит через точку (4;0) и параллельно оси ординат (ОY).
Подробнее - на -
b5=10*3^5=2430
q=3