Объяснение:
Чтобы решить эту задачу, нужно знать как минимум 2 операции с матрицами:
Сложение/вычитание матриц. Если у тебя есть матрица A с элементами
(т.е. на i строке j столбца находится число ), и некоторая другая матрица той же размерности B с элементами 
, то в итоговой матрице C = A + B элементы 
, с вычитанием все то же самое, только разность a и b. На практике это выглядит как сумма (или разность) соответствующих чиселУмножение матриц на некоторую константу. Если умножать матрицу A с элементами на некоторое постоянное число C, то C*A =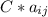 
, т.е. умножаете это число на каждый элемент матрицы.Теперь давайте найдем по условию 3A
![3A = \left[\begin{array}{cc}12&-3\\9&6\end{array}\right]](/tpl/images/0988/6779/046d9.png)
Теперь 2B:
![2B = \left[\begin{array}{cc}-4&2\\10&6\end{array}\right]](/tpl/images/0988/6779/f0fc3.png)
Теперь поэлементно из одного вычитаем другое:
![C = 3A - 2B = \left[\begin{array}{cc}16&-5\\-1&0\end{array}\right]](/tpl/images/0988/6779/e2957.png)
(х + 3)/(х - 7) - 6/(х + 7) = 140/(х² - 49),
(х + 3)(х + 7)/(х² - 49) - 6(х - 7)/(х² - 49) = 140/(х² - 49),
(х² + 7х + 3х + 21)/(х² - 49) - (6х - 42)/(х² - 49) = 140/(х² - 49),
(х² + 7х + 3х + 21 - 6х + 42)/(х² - 49) = 140/(х² - 49),
(х² + 7х + 3х + 21 - 6х + 42 - 140)/(х² - 49) = 0,
(х² + 4х - 77)/(х² - 49) = 0,
ОДЗ:
х² - 49 ≠ 0,
(х - 7)(х + 7) ≠ 0,
х - 7 ≠ 0, х + 7 ≠ 0,
х ≠ 7, х ≠ -7,
х² + 4х - 77 = 0,
Д = 4² - 4*1*(-77) = 16 + 308 = 324,
х1 = (-4 + 18) / 2*1 = 14 / 2 = 7,
х2 = (-4 - 18) / 2*1 = -22 / 2 = -11,
ответ: х = -11
х²-2х-63=0
D=4+4*63=256=16²
x₁=(2-16)/2=-7
x₂=(2+16)/2=9
Это число либо -7 либо 9