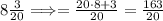
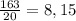
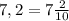
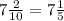
уравнение с параметром просто как и в обыкновенном кв. уравнинии вот найди дискриминант и корни уравн
дискриминант=4a^2-4(a-2)(2-3a)=4a^2-4(2a-3a^2-4+6a)=4a^2-8a+12a^2+16-24a=16a^2-32a+16=(4a-4)^2
-2a+корень из (4a-4)^2 -2a+4a-4 2a-4
x1====1
2(a-2) 2a-4 2a-4
первый корень x1=1
-2a-корень из (4a-4)^2 -2a-4a+4 -6a+4 2(-3a+2) 2-3a
x2=== =
=
2(a-2) 2(a-2) 2(a-2)
( 5x-1)^2=0
5x-1=0
5x=1
x=1/5
2),3) - не знаю
4) x^2-5x=0 (вынесение общ.множ.)
x*(x-5)=0
x1=0, x2=5
5) -x^2=-8
x^2=8
x1=
x2=
6) 16x^2+24x+9=0 (формула сокр.умнож.)
(4x+3)^2=0
4x+3=0
x=-3/4
7) 3x^2-4x+2=0
D=16-4*3*2<0
нет корней
8) x^2-11x-42=0
D=121-4*1*(-42)=289=17^2
x1=(11+17)/2=14
x2=(11-17)/2=-3
9) x^2-12x+35=0 (теорема виета)
x1=5
x2=7
10) x^2-14x+48=0 (теорема виета)
x1=6
x2=8