Question

Периметр прямокутника дорівнює 28см, а його площа 40см2. знайти сторони прямокутника.

Answer 1

Придётся решать систему двух уравнений:
х + у = 14
ху = 40  ( х и у - стороны прямоугольника)
Сделаем подстановку: х = 14 - у
у(14 - у) = 40
14у - у² = 40
у² -14 у +40 = 0
По т. Виета у1 = 10 и у2 = 4
                    х1 = 4    и  х2 = 10
ответ: 10 и 4

Answer 2

Объяснение:

Дано:

P = 28 см

S = 40 см²

a - ?

b - ?

Периметр прямоугольника:

P = 2·(a + b)        (1)

Площадь прямоугольника:

S = a·b                (2)

Получили систему уравнений (1) и (2)

2·(a + b) = 28

a·b = 40

Получили:

a + b = 28/2       (3)

a·b = 40             (4)

a + b = 14;       →  b = 14 - a;

Подставляем в (4)

a·b = 40 ;      a·(14 - a) = 40;

14a - a² = 40

a² - 14a + 40 = 0

Решаем это квадратное уравнение:

a₁ = 10 см:      b₁ = 4 см

или

a₂ = 4 см:      b₂ = 10 см

Answer 3

10 см - длина и 4 см - ширина прямоугольника

Объяснение:

Перевод: Периметр прямоугольника равен 28 см, а его площадь 40 см². Найти стороны прямоугольника.

Дано:

 ABCD - прямоугольник

 P(ABCD) = 28 см

 S(ABCD) = 40 см²  

Найти: стороны прямоугольника.

Решение.

Пусть сторонами прямоугольника будут a и b, для определённости, a - длина и b - ширина (см. рисунок). По определению прямоугольника: a≥b.

Периметр прямоугольника определяется по формуле

P(ABCD) = 2·(a + b),

а площадь - по формуле

S = a·b.

На основе данных получим следующую систему уравнений:

$\displaystyle \tt \left \{ {{2 \cdot (a+b)=28} \atop {a \cdot b=40}} \right. \Leftrightarrow \left \{ {{a+b=14} \atop {a \cdot b=40}} \right. \Leftrightarrow \left \{ {{a=14-b} \atop {(14-b) \cdot b=40}} \right.$

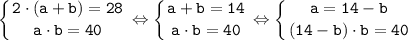
Сначала решаем второе квадратное уравнение системы:

(14 - b)·b = 40 ⇔ 14·b - b² = 40 ⇔ b² -14·b + 40=0

D=(-14)² - 4·1·40 = 196 - 160 = 36 = 6²:

b₁=(14-6)/(2·1)= 8/2=4;

b₂=(14+6)/(2·1)=20/2=10.

Тогда

$\displaystyle \tt \left \{ {{a_1=14-4=10, a_2=14-10=4} \atop {b_1=4, b_2=10}} \right. .$

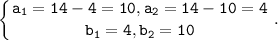
Но, по определению прямоугольника: a≥b. И поэтому ответом будет пара 10 и 4.