ответ: при a ∈ (-7/4; 1/2].
Объяснение:
Пусть 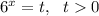 , тогда получаем уравнение
, тогда получаем уравнение
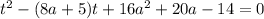 (*)
(*)
D = (8a+5)² - 4(16a² + 20a - 14) = 64a² + 80a + 25 - 64a² - 80a+56 = 81
Используем теорему Виета
x₁ + x₂ = 8a + 5
x₁x₂ = 16a² + 20a - 14
Исходное уравнение имеет одно решение, если корни квадратного уравнения (*) имеют разные знаки. Это возможно, когда :
16a² + 20a - 14 < 0
8a² + 10a - 7 < 0
(4a + 7) * (4a-2) < 0
+++++++++(-7/4)------------(1/2)+++++++++++
Но, если подставить a=1/2, получим одно решение.
При a ∈ (-7/4; 1/2] уравнение имеет одно решение.
х²-9=0
х≠+-3
x₁=3 не подходит по ОДЗ
ответ х=-4
b)ОДЗ
х-2≠0
х≠2
х-3≠0
х≠3
ЗАДАЧА:
Переведем минуты в часы: 10 мин=10/60 ч=1/6 часа
27-7=20 км обратный путь велосипедиста
Пусть скорость велосипедиста из пункта в А в В составляет х км/ч. А время на дорогу 27/х часов. Тогда, поскольку он уменьшил скорость на обратном пути на 3 км/ч, то скорость (х-3) км/ч велосипедиста на обратном пути. При этом время он потратил 20/(х-3) часов. Известно, что разница во времени составляет 1/6 часа. Составим и решим уравнение.
27/х-20/(х-3)=1/6
(27(х-3)-20х)/х(х-3)=1/6
6*(27х-81-20х)=х²-3х
6(7х-81)=х²-3х
х²-3х=42х-486
x²-45x+486=0
D=45²-486*4=81=9²
х₁=(45-9)/2=18 км/ч
х₂=(45+9)/2=27 км/ч
Значит велосипедист ехал из А в В либо со скоростью 18 км/ч, либо со скоростью 27 км/ч.
Проверка:
1) x=18 км/ч
27/18-20/15=1/6
1/6=16
2) х=27 км/ч
27/27-20/24=1/6
1/6=1/6
ответ велосипедист ехал из А в В либо со скоростью 18 км/ч, либо со скоростью 27 км/ч.