-6,7059
Объяснение:
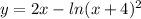
Сначала находим производную нашей функции
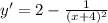
Затем приводим функцию к нулю, превратив его в уравнение
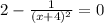
Область допустимых значений (ОДЗ) нашего уравнения ровна
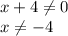
Упрощаем уравнение, домножив обе части на 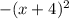
Получаем 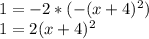
Упростим уравнение 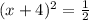
Возведем обе части под корень, чтоб избавиться от квадрата
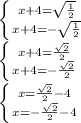
x≈ -3.29 и x≈-4.70
Делаем проверку ОДЗ
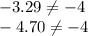
Оба выражения верны, следовательно чертим числовую прямую
\\\\\\\\\\\\\\\\\\\\\\\\\•\\\\\\\\\\\\•ххххххххх•ххххххх•////////////////////////////→
-4.70 -3.5 -3.29 0
Нам подходит только x≈-3.29
Теперь в саму функцию подставляем x
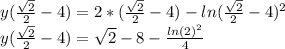
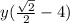 ≈
≈ 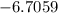
ответ: Наибольшее значение функции y=2x-ln(x+4)^2 на отрезке [-3,5;0] равно -6,7059
В решении.
Объяснение:
Сравнить выражения, если c > d:
а) 0,3с и 0,3d
На примере:
с=3, d=2 c > d
0,3 * 3 > 0,3 * 2
То есть, если множитель при с и d одинаковый, то произведение множителя на с будет больше произведения множителя на d, потому что с > d по условию (если множитель положительный).
0,3с > 0,3d
б) -0,5с и -0,5d
Здесь наоборот, так как числа в результате умножения отрицательные, то чем больше число по величине, тем оно меньше из-за того, что отрицательное.
На примере:
с=3, d=2 c > d
-0,5 * 3= -1,5
-0,5 * 2= - 1
-1,5 < - 1
В данном случае -0,5с < -0,5d
(8x-y)^2-64x^2=64x^2-y^2-64x^2=-y^2
2(a-b)^2=2(a^2-2ab+b^2)=2a^2-4ab+2b^2
-y(3x-y)^2=-y(9x^2-6xy+y^2)=-9x^2y+6xy^2-y^3
a(4-a)+(4-a)^2=4a-a^2+16-8a+a^2=-4a+16=-a+4