Наиболее сложное решение:
Пусть x - количество бензина в первой бочке, а y - во второй. По условию задачи составим систему уравнений:
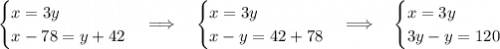
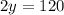
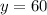 (л) - бензина во второй бочке
(л) - бензина во второй бочке
60 · 3 = 180 (л) - в первой бочке
Решение через уравнение (рационально):
Пусть x - количество бензина во второй бочке, тогда в первой - 3x. По условии задачи составляем уравнение:
3x - 78 = x + 42
3x - x = 42 + 78
2x = 120
x = 60 (л) - во второй бочке
60 · 3 = 180 (л) - в первой бочке
ответ: в первой бочке 180 л бензина, во второй - 60 л.
Задача может быть простой, даже несмотря на тему (здесь нельзя решить сложнее, чем в первом варианте)
4
Запишем условие:
lgx + lg(x - 2) = lg(12 - x)
Складываем логарифмы в левой части, тогда:
lgx(x - 2) = lg(12 - x)
Так как 1 основание, решаем как обычное уравнение:
х(х - 2) = 12 - х
Раскороем скобки слева, откуда:
х^2 - 2х = 12 - х
Переносим правую часть влево, тогда:
х^2 - 2х - 12 + х = 0
Приводим подобные:
х^2 - х - 12 = 0
Решаем через дискриминант:
Находим дискриминант:
D = b^2 - 4ac
D = 1 - 4*1*(-12)
D = 1 - (-48)
D = 1 + 48 = 49
sqrt(D) = sqrt(49) = 7
x1 = (-b + sqrt(D))/2a = (1 + 7)/2 = 8/2 = 4
x2 = (-b - sqrt(D))/2a = (1 - 8)/2 = -3,5 - посторонний корень
Проверка:
Проверяем х1:
lg4 + lg(4 - 2) = lg(12 - 4)
lg4 + lg2 = lg8
Складываем логарифмы слева, тогда:
lg(4*2) = lg8
lg8 = lg8
Следовательно, х1 является действительным (правильным) корнем уравнения.
Проверяем х2:
lg(-3,5) + lg(-3,5 - 2) = lg(12 - 3,5)
lg(-3,5) + lg(-5,5) = lg8,5
Складываем логарифмы в левой части, тогда:
lg(19,25) > lg8,5
Следовательно, х2 посторонний корень данного уравнения.
Sn=b1*(1-q^n)/(1-q)
S5=8*[1-(1/2)^5)/(1-1/2)=8*(1-1/32)/(1/2)=8*31/32*2=496/32=15,5
ответ: S5=15,5