1) - 8b^2 + c + bc - 2b^2 - 6bc + 3c + 5bc=-10b^2+4c=-10+3=-7
2) x - 100%- оптовая цена
1.2x - 120% - розничная цена
1.2x - 100%
1,08x - 90% - рекламная цена
1.08x-x=10.8
0.8x=10.8
x=13.5
ответ: 13 рублей 50копеек - оптовая цена
3) а) 3/8a^3b^2 * 6 ab^2 * (-4b) = -9a^4b^5
б) 12x^4y^5 * (-5xy^3)^2 = -300x^6y^11
4) B=A^n
B = 128x^14y^21z^7, n = 7
B=(2x^2y^3z)^7
A=2x^2y^3z
5) пусть а - ребро меньшего куба, тогда 2а - ребро большего куба
a^3+8a^3=1125
9a^3=1125
a^3=125
a=5
ответ: 5дм - ребро меньшего куба
Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
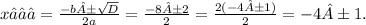
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
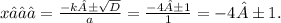
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
1)lg x =2-lg5 ОДЗ: x>0
lg x+lg5=2
lg5x=2
5x= 10^2
5x=100
x=20
2) lgx + lg (x-15) =2 ОДЗ: x>0; x>15
lg x(x-15)=lg 100
x(x-15)=100
x^2-15x-100=0
D=(-15)^2-4*1*(-100)=625
x1=(15-25)/2= -5 - посторонний корень,не входящий в ОДЗ
x2= (15+25)/2=20
ответ:20