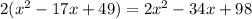
Пусть x - сумма всех учеников в первой группе до перехода, а y - количество учеников в этой группе. Тогда:
x/y = 22
Пусть k - сумма всех учеников во второй группе до перехода, а l - количество учеников в этой группе. Тогда:
k/l = 45
Известно, что при переходе ученика из второй группы в первую, средний у обоих групп повысился на 1, то есть:
(x+n)/(y+1)=23
(k-n)/(l-1)=46
Где n - количество ученика, который перешёл из второй группы в первую. Выразим n в обеих формулах:
n = 23(y+1)-x
n = -46(l-1)+k
Приравняем правые части этих уравнений:
23(y+1)-x = -46(l-1)+k
23y+23-x = k-46l+46
x и k мы можем выразить из двух первых формул, то есть:
x = 22y
k = 45l
Подставим правые части данных уравнений в уравнение выше:
23y+23-x = k-46l+46
23y+23-22y = 45l-46l+46
y+23 = 46-l
y+l = 46-23
y+l = 23
Поскольку y - количество учеников в первой группе, а l - количество учеников во второй группе, то y + l = 23 ученика в обеих группах.
23 ученика в обеих группах
1) 6 км/ч; 2) 27 км/ч
Объяснение:
Пусть х - собственная скорость катера
х + 3 - скорость катера по течению реки
х - 3 - скорость катера против течения реки
По условию
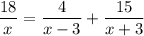
18(x² - 9) = 4x(x + 3) + 15x(x-3)
18x² - 162 = 4x² + 12x + 15x² - 45x
x² - 33x + 162 = 0
D = 33² - 4 · 162 = 441 = 21²
x₁ = 0.5 (33 -21) = 6 (км/ч)
х₂ = 0,5 (33 + 21) = 27 (км/ч)
По смыслу задачи и то и другое число подходит. Проверим.
1) 6 км/ч
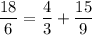
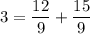
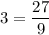
3 ≡ 3 (верно!)
2) 27 км/ч
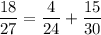
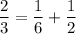
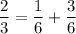
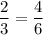
2/3 ≡ 2/3 (всё верно)
При движении с собственной скоростью 6км/ч путь займет у катера 3 часа, а при движении со скоростью 27 км/ч путь займёт 2/3 ч = 40 мин.