Рассчитай расстояние вершины куба до диагонали куба, которая не проходит через эту вершину, если ребро куба — 45 см
Объяснение:
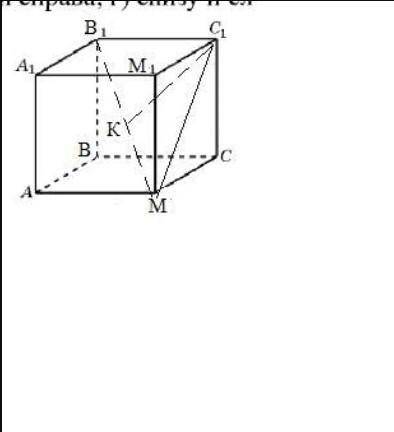
Пусть АВСМА₁В₁С₁М₁-куб, АВ=45см. Все грани равные квадраты.Расстоянием от вершины С₁ до диагонали В₁М будет длина перпендикуляра С₁К.
Найдем диагональ квадрата по т. Пифагора ⇒ 45√2 см.
Найдем диагональ куба d²=45²+45²+45² , d²=3*45² , d=45√3 см.
ΔМВ₁С₁- прямоугольный, т.к. проекция М₁С₁⊥ В₁С₁ , то и наклонная МС₁⊥В₁С₁ по т. о трех перпендикулярах. Используя формулу площади треугольника :
S(В₁С₁М)=1/2*В₁С₁*С₁М или S(В₁С₁М)=1/2*В₁М*С₁К ⇒
S(В₁С₁М)=1/2*45*45√2 , подставим во вторую формулу, получим :
1/2*45*45√2=1/2*45√3*С₁К или С₁К=(45√2)/√3=(45√6)/3=15√6 (см)
х км – расстояние от дома до остановки
х/6 час – время от дома до остановки
54 мин = 54/60 ч = 9/10 ч
9/10 – х/6 = (27 – 5х)/30 час – время на троллейбусе от остановки до школы.
30 * (27-5х)/30 = (27 – 5х) км – расстояние от остановки до школы
На обратном пути расстояние (27 – 5х) он проехал со скоростью 36 км/ч.
(27 – 5х)/36 час – время от школы до остановки
А расстояние х км со скоростью 5 км/ч.
х/5 ч – время от остановки до дома
56 мин = 56/60 ч = 14/15 ч
Уравнение:
(27 – 5х)/36 + х/5 = 14/15
Умножим уравнение на 180 и получим:
5(27 – 5х) + 36х = 168
135 – 25х + 36х = 168
11х = 33
х = 33 : 11
х = 3 км - расстояние от дома до остановки
27 – 5 * 3 = 27 – 15 = 12 км – расстояние от остановки до школы
3 + 12 = 15 км - всё расстояние