Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
А) f(x) = x² - 7x + 10
x² - 7x + 10 = 0
Корни уравнения находим по теореме Виета:
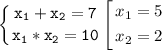
ответ: x₁ = 5, x₂ = 2
Б) f(x) = -x² + 5x - 7
-x² + 5x - 7 = 0
D = b² − 4ac = 5² - 4 * (-1) * (-7) = 25 - 28 = -3
ответ: нулей нет, т.к. D < 0
В) f(x) = 2x² - 8x - 8
2x² - 8x - 8 = 0
D = b² − 4ac = 64 + 4 * 2 * 8 = 64 + 64 = 128
![\tt\displaystyle x_{1;2}=\frac{-b\pm\sqrt[]{D}}{2a}=\frac{8\pm\sqrt[]{128}}{4}=\frac{8\pm8\sqrt{2}}{4} \\\\x_{1}= \frac{8+8\sqrt{2}}{4}=2+2\sqrt{2}\\\\x_{2}=\frac{8-8\sqrt{2}}{4}=2-2\sqrt{2}](/tpl/images/0029/9864/7f8dc.png)
ответ: x₁ = 2 + 2√2, x₂ = 2 - 2√2.
Г) f(x) = 6x² - 5x + 1
6x² - 5x + 1 = 0
D = b² − 4ac = 25 - 4 * 6 * 1 = 25 - 24 = 1
![\tt\displaystyle x_{1;2}=\frac{-b\pm\sqrt[]{D}}{2a}=\frac{5\pm\sqrt{1}}{12}=\frac{5\pm1}{12}\\\\x_{1}= \frac{5+1}{12}=\frac{6}{12}=\frac{1}{2} \\\\x_{2}=\frac{5-1}{12}=\frac{4}{12}=\frac{1}{3}](/tpl/images/0029/9864/54b54.png)
ответ: x₁ = 1/2, x₂ = 1/3.