-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
Обозначим длину одного катета а, второго - b.
Площадь прямоугольного треугольника находится по формуле:
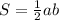 ,
,
где а, b - катеты.
В нашем случае:
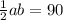
Отсюда аb=90:(1/2)
аb=90*2
ab=180
На каждом катете построили квадрат, затем нашли площади этих квадратов и полученные результаты сложили.
Чтобы найти площадь квадрата, нужно возвести длину его стороны во вторую степень. Площадь квадрата, построенного на катете а будет равна а². Площадь квадрата, построенного на катете b будет равна b². Складываем площади двух квадратов:
а²+b²=369
Из полученных двух уравнений с двумя неизвестными составляем систему:
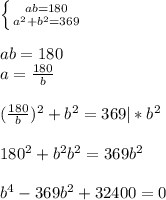

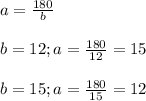
ответ: катеты прямоугольного треугольника равны 12 см и 15 см.