sin x + cos x = 1;
Возведем правую и левую часть выражения в квадрат, тогда получим:
(sin x + cos x) ^ 2 = 1 ^ 2;
sin ^ 2 x + 2 * sin x * cos x + сos ^ 2 x = 1;
(sin ^ 2 x + cos ^ 2 x) + 2 * sin x * cos x = 1;
Так как, по формуле тригонометрии sin ^ 2 x + cos ^ 2 x = 1 и 2 * sin x * cos x = sin (2 * x), тогда получим:
1 + 2 * sin x * cos = 1;
2 * sin x * cos x = 1 - 1;
2 * sin x * cos x = 0;
sin x * cos x = 0;
1) sin x = 0;
x = pi * n, где n принадлежит Z;
2) cos x = 0;
x = pi / 2 + pi * n, где n принадлежит Z.
1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
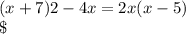
Переобразуем:
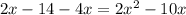
Переносим в общую сторону (левую) и меняем знаки:
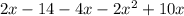
Сокрашаем:
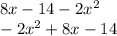
ответ: 
Старший коэффициент: 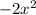
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А) 
В) 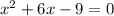
С) 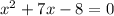
D) 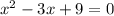
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
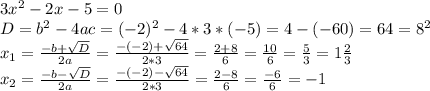
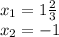
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
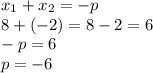


ответ: 
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят  и
и 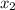 совпадают.
совпадают.
Если p = 0, то 

ответ: c = 32
3. б) Найдите эти корни уравнения
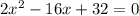
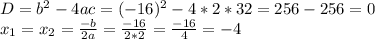
ответ: 
х - меньший угол;
(х + 15) - больший угол.
х + х + 15 = 90
2х + 15 = 90
2х = 90 - 15
2х = 75
х = 37,5 - меньший угол.
37,5 + 15 = 52,5 - больший острый угол.
ответ: 52,5°.