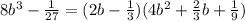1. представить в виде многочлена стандартного вида выражение (а+3)^2+(а-3)(а+3)+6а 2. разложить на множители: а) (2-3n)^2-9n^4 б) (а-5)^2+2(5-а)+1 в) х^6-х^4-х^2+1 г) 8b^2-1/27(это одна двадцать восьмая) если что ^2 это степень
Числа вида 4n, 4n+1 и 4n+3 представимы в виде разности квадратов: 4n=(n+1)²-(n-1)²; 4n+1=(2n+1)²-(2n)²; 4n+3=(2n+2)²-(2n+1)².
Числа вида 4n+2 не представимы в виде разности квадратов, т.к. иначе 4n+2=a²-b²=(a-b)(a+b). Если а и b имеют разную четность, то а-b и a+b - нечетные числа, и значит (a-b)(a+b) нечетно. Если а и b имеют одинаковую четность, то а-b и a+b - оба четные, и значит (a-b)(a+b) делится на 4. Но число 4n+2 - не является нечетным и не делится на 4. Значит, оно не может быть равно a²-b² ни при каких а и b.
Таким образом, все натуральные числа не представимые в виде разности квадратов имеют вид 4n+2, где n=0,1,2, Так как первое такое число (равное 2) будет при n=0, то трехтысячное число будет при n=2999, т.е. равно 4*2999+2=11998.
1.
(a + 3)² + (a - 3)(a + 3) + 6a =
= a² + 6a + 9 + a² - 9 + 6a = 2a² + 12a
2.
а) (2 - 3n)² - 9n⁴ = (2 - 3n)² - (3n²)² = (2 - 3n - 3n²)(2 - 3n + 3n²)
б) (a - 5) ² + 2(5 - a) + 1 = (a - 5)² - 2(a - 5) + 1 = ((a - 5) - 1)² = (a - 6)²
в) x⁶ - x⁴ - x² + 1 = x⁴(x² - 1) - (x² - 1) = (x² - 1)(x⁴ - 1) = (x² - 1)(x² - 1)(x² + 1) =
= (x² - 1)²(x² + 1) = (x - 1)²(x + 1)²(x² + 1)
г)