Алгебра: Докажите неравенство (х+7)^2больше чем х(х+14)

Докажите неравенство (х+7)^2больше чем х(х+14)

👇

Увидеть ответ

Ответ:

prozorovamary23

28.02.2023

(х+7)^2=х^2+14х+49=х(х+14)+49.
х(х+14)+49>х(х+49) чтд.

4,6(76 оценок)

Открыть все ответы

Ответ:

природа45

28.02.2023

ответ: 6 л .

Пусть 8 литров водного раствора кислоты содержит х литров салициловой кислоты.

Тогда в этом растворе кислоты будет х/8 частей.

Добавили ещё 16 л раствора, в которых содержится 60% кислоты, то есть кислоты там будет 16*0,6=9,6 л .

Теперь есть (8+16)=24 л раствора, в котором содержится (х+9,6) л кислоты . Значит кислоты содержится (х+9,6)/24 частей .

Но в результате кислоты стало на 10% меньше , чем было, то есть стало (х/8-0,1) частей кислоты . Составим уравнение .

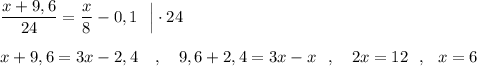
$\dfrac{x+9,6}{24}=\dfrac{x}{8}-0,1 \ \ \Big|\cdot 24\\\\x+9,6=3x-2,4\ \ \ ,\ \ \ 9,6+2,4=3x-x\ \ ,\ \ \ 2x=12\ \ ,\ \ x=6$

Изначальный объём кислоты в восьмилитровом растворе был равен

6 литрам .

Проверим вычисления. 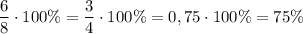$\dfrac{6}{8}\cdot 100\%=\dfrac{3}{4}\cdot 100\%=0,75\cdot 100\%=75\%$

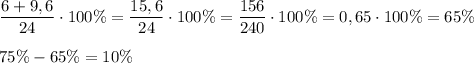
$\dfrac{6+9,6}{24}\cdot 100\%=\dfrac{15,6}{24}\cdot 100\%=\dfrac{156}{240}\cdot 100\%=0,65\cdot 100\%=65\%\\\\75\%-65\%=10\%$

4,4(49 оценок)

Ответ:

gilev2004stepaxa

28.02.2023

Дробь — это выражение вида рq , где р и q — многочлены; р — числитель, а q — знаменатель дроби. например: a−bb 2−1 где p = a−b , а q = b 2−1 ; x 2+3y 3+x где p = x 2+3 , а q = y 3+x ; y 2−1y−1 где p = y 2−1 , а q = y−1 . многочлен — это частный случай дроби. например, многочлен y 3+2y+7 равен дроби y 3+2y+71 , а дробь 3x 2+5x−15 можно записать в виде многочлена 35x 2+x− 15 . из курса мы знаем, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. например: 35 = 3•25•2 = 610 . дроби можно преобразовывать аналогичным способом: числитель и знаменатель дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной дроби; числитель и знаменатель дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной дроби, его называют сокращением дроби. данные правила называют основным свойством дроби. рассмотрим примеры. дробь x 2−xx 2 можно заменить на x−1x (числитель и знаменатель разделили на x ). дробь x 2+3xy+1 можно заменить на x 3+3x 2xy+x (числитель и знаменатель умножили на x ). дробь y 2−6y+9y 2−9 можно заменить на (y−3) 2(y−3)(y+3) = y−3y+3 (числитель и знаменатель разделили на y−3 ). равенство y 2−6y+9y 2−9 = y−3y+3 называется тождеством, а преобразование дроби y 2−6y+9y 2−9 в дробь y−3y+3— тождественным преобразованием заданной дроби, в данном случае, сокращением дроби. следует помнить, что тождеством наше равенство является при условии, что y ≠ 3 и y ≠ – 3 , так как знаменатель изначальной дроби при данных значениях переменной обращается в нуль и выражение y 2−6y+9y 2−9 теряет смысл.

4,6(59 оценок)

Это интересно:

Питомцы-и-животные

21.04.2022

Как выращивать кроликов ради мяса или шерсти...

Хобби-и-рукоделие

07.07.2021

Как сделать светящуюся палочку: пошаговая инструкция...

Дом-и-сад

03.02.2020

Как быстро и эффективно избавиться от шоколадных пятен...

Искусство-и-развлечения