Так как в уравнении есть квадратные корни, то запишем ОДЗ:
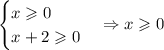
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
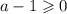
Таким образом, при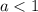 
уравнение не имеет корней.
Предположим, что . Тогда:
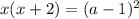
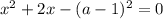
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
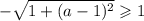
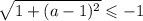
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра 
.
Для второго корня получим:
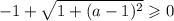
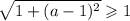
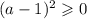
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
при 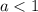: нет корней,
при : 
Пусть ромб будет АВСD, АС = 10 cм,AB=13см, О -- т. перес. диаг.
Поэтому тр-к АВО - прямоуг.
АВ^{2} = АО^{2} + ВО^{2}
АО= АС/2=5
169 = 25 + ВО^{2}
ВО^{2} = 144
ВО =12
ВD = 2*ВО = 2*12 = 24 (cм) - это и есть вторая диагональ.
ответ: 24 cм.