экстремумы (sin a - cos a) найдем, приравняв к нулю производную:
cos a + sin a = 0
sin a = -cos a - решение в точках 3pi/4 + n*pi, n принадлежит Z
в точках 3pi/4 + 2n*pi, n принадлежит Z, sin a = (корень из 2)/2, cos a = -(корень из 2)/2, значит (корень из 2)/2 * sin a - (корень из 2)/2 * cos a = 2/4 - (-2/4) = 1 - максимум исходной функции.
в точках -pi/4 + 2n*pi, n принадлежит Z, sin a = -(корень из 2)/2, cos a = (корень из 2)/2, значит (корень из 2)/2 * sin a - (корень из 2)/2 * cos a = - 2/4 - 2/4 = -1 - минимум исходной функции.
Из вышесказанного можно сделать вывод, что исходное выражение будет лежать в данном интервале при любом значении альфа.
Если f(- x) = f(x) , то функция чётная
Если f(- x) = - f(x) , то функция нечётная
1) f(x) = - 3x³ + 1
f (- x) = - 3 * (- x)³ + 1 = 3x³ + 1
f(x) ≠ f(- x) - значит функция не является чётной
- f(x) = - (- 3x³ + 1) = 3x³ - 1
f(- x) ≠ - f(x) - значит функция не является нечётной
ответ : f(x) = - 3x³ + 1 - не чётная и не нечётная
2) f(x) = 1/6 - 6x²
f(- x) = 1/6 - 6 * (-x)² = 1/6 - 6x²
f(x) = f(- x) - значит функция чётная
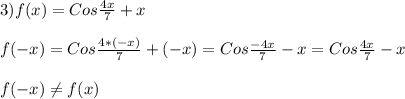
Значит функция не является чётной
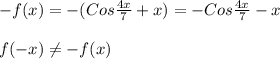
Значит функция не является нечётной
ответ : Функция не чётная и не нечётная