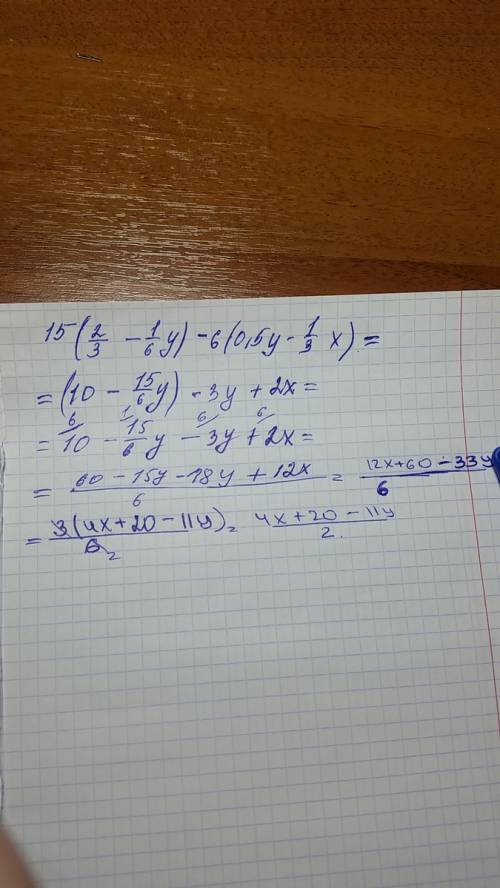
целые решения уравнения это делители свободного члена.
Можно подставлять все делители свободного члена, но нам нужно только 2, если уравнение 4 степение, и 3 если уравнение 5 степени(так как в этом случае мы разложим ее в таком виде (x-x1)(x-x2)(ax^2+bx+c)=0, а такое уравнение решить легко).
в первом это числа -2 и 3.
получаем x^4-x^3-5x^2-x-6=(x-3)(x+2)(x^2+1). теперь нужно каждый множитель приравнять нулю решить уравнения а потом обьеденить все корни:
x-3=0 => x=3; x+2=0 => x=-2; x^2+1=0 нет корней. ответ: -2; 3
а другие уравнения напиши в другой теме. по правилам сайта
Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач.
у/5.
Объяснение:
Упростите выражение:
(x+4)/(x-3) * (3x-9)/(x²+8x+16) : 15/(xy+4y)=
1)(x+4)/(x-3) * (3x-9)/(x²+8x+16)=
В числителе второй дроби вынести 3 за скобки, в знаменателе второй дроби квадрат суммы, свернуть:
=(x+4)/(x-3) * [3(x-3)]/(x+4)²=
Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй, а знаменатель первой дроби умножить на знаменатель второй:
=[(x+4)*3(x-3)] / [(x-3)*(x+4)(x+4)]=
сокращение (x+4) и (x+4) на (x+4), (x-3) и (x-3) на (x-3):
=3/(x+4);
2)3/(x+4) : 15/(xy+4y)=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
=[3*у(x+4)] / [(x+4)*15]=
сокращение (x+4) и (x+4) на (x+4), 3 и 15 на 3:
=у/5.