Решение вашего задания
Объяснение:
-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
Если одночлены состоят из одинаковых переменных в одинаковых степенях, то они являютсяподобными. Коэффициенты одночленов при этом могут различаться. Примеры подобных одночленов:
3a2 и –4a2; 31 и 45; a2bx4 и 1,4a2bx4; 100y3и 100y3
Но одночлены –6ab2 и 6ab не являются подобными, так как у них переменная b находится в разных степенях.
Подобные одночлены обладают удивительным свойством — их можно легко складывать и вычитать. Если нужно найти сумму двух или более подобных одночленов, то их коэффициенты надо сложить, а переменные в сумме оставить без изменений. Если же требуется найти разность двух подобных одночленов, то коэффициент одного одночлена надо вычесть из второго, а переменные оставить без изменений. Примеры:
4x2 + 15x2 = 19x2
5ab – 1,7ab = 3,3ab
13a10b5c3 – 13a10b5c3 = 0a10b5c3 = 0
Эти действия называются приведением подобных одночленов.
Почему же подобные одночлены можно так складывать и вычитать? Попробуем упростить выражения, не используя правила приведения подобных одночленов:
2x + 4x = (x + x) + (x + x + x + x) = x + x + x + x + x + x = 6 * x = 6x
2x – 4x = (x + x) – (x + x + x + x) = x + x – x – x – x – x = – x – x = – (x + x) = –(2x) = –2x
То есть свойство подобных членов вытекает из правила арифметики о том, что произведение двух чисел является ничем иным как суммой из слагаемых одного числа, где количество слагаемых равно другому числу:
2 * 3 = 3 + 3 = 2 + 2 + 2
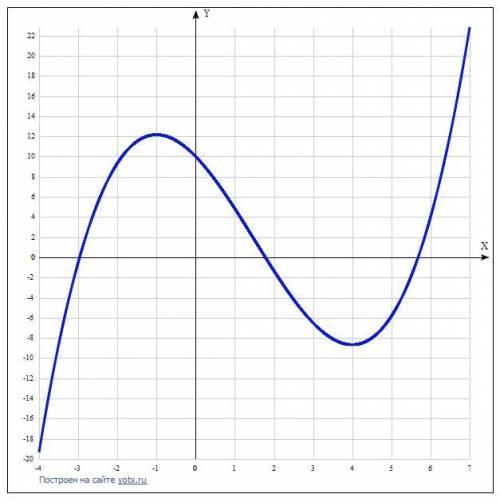
Дана функция у = (1/3)х³ - (3/2)х² - 4х + 10.
Исследование функций по схеме:
1. Область определения функции : ограничений нет, х ∈ R.
2. Непрерывность функции, вертикальные асимптоты: разрывов функции нет, значит, функция непрерывна. Поэтому и вертикальных асимптот нет.
3. Точки пересечения функции с осями координат.
С осью Оу при х = 0. Это точка (0; 10).
С осью Ох при у = 0.
Надо решить уравнение (1/3)х³ - (3/2)х² - 4х + 10 = 0.
Для решения кубического уравнения используем метод Кардано - Виета. Приводим его к виду
х³ - 4,5х² - 12х + 30 = 0. Делаем подстановку у = х – (а/3). Получаем уравнение неполного вида:
у3 + py + q = 0. Корни вычисляются по тригонометрической формуле Виета.
Они являются абсциссами точек пересечения оси Ох:
x₁ = 5,682681
x₂ = -2,963867
x₃ = 1,781186
4. Четность, нечетность.
f(-х) у = (1/3)(-х)³ - (3/2)(-х)² - 4(-х) + 10 = у = -(1/3)х³ - (3/2)х² + 4х + 10 ≠ f(x), ≠ -f(x).
Функция не чётная и не нечётная.
5. Периодичность: не периодическая.
6. Промежутки возрастания, убывания, экстремумы функции.
Находим производную: y' = ((1/3)х³ - (3/2)х² - 4х + 10)' = х² – 3x – 4.
Приравниваем её нулю: х² – 3x – 4 = 0. D = 9 + 4*4 = 25.
x1 = (3 – 5)/2 = -1, x2 = (3 + 5)/2 = 4.
Имеем 2 критических точки: х = -1 и х = 4.
Находим знаки производной на полученных промежутках.
х = -2 -1 1 4 5
y' = 6 0 -6 0 6
Видим, что при прохождении через точкe х = 4 производная меняет знак с минуса на плюс, то есть это будет минимум, а при прохождении через точку х = -1 меняет знак с плюса на минус, соответственно это будет максимум.
Промежутки возрастания (y' > 0): (-∞; -1) и (4; +∞).
Убывания: (-1; 4) .
7. Промежутки выпуклости, вогнутости, точки перегиба.
Вторая производная равна y'' = 2x - 3. Приравняем нулю:
2x - 3 = 0. х = 3/2. Это и есть точка перегиба.
8. Наклонные асимптоты: нет.
9. Построение графика. Таблица точек:
x y
-4 -19.3
-3 -0.5
-2 9.3
-1 12.2
0 10
1 4.8
2 -1.3
3 -6.5
4 -8.7
5 -5.8
6 4
7 22.8