Question

Виктор михайлович положил в банк 96000 рублей. несколько лет ему начислялись то 5 %, то 10%, а за последний год начислили 25% годовых, при этом проценты начислялись в конце каждого года и добавлялись к сумме вклада. в результате его вклад стал равным 160 083 рублей. сколько лет пролежал вклад в банке?

Answer 1

Получать 5% годовых n лет означает умножить на $1,05^n$
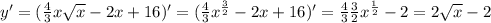
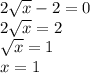
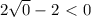
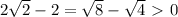
получать 10% годовых m лет означает умножить на $1,1^m$
получать 25% годовых 1 год означает умножить на 1,25
m и n - натуральные числа (1,2,3,4...)

получаем уравнение
$96000*1,05^n*1,1^m*1,25= 160 083$

Решать придется подбором

$1,05^n*1,1^m=1,334025 \\ 1,05^{n-1}*1,1^{m-1}=1,334025/(1,05*1,1) \\ 1,05^{n-1}*1,1^{m-1}=1,155 \\ 1,05^{n-2}*1,1^{m-2}=1$

m=2 и n=2
ответ: вклад пролежал в банке 5 лет