допустим что стороны прямоугольника A и B, и площадь S. Тогда S=A*B (площадь равно произведению сторон). Далее сказано, что одна сторона больше другой на 11 см. доопустим A=B+11. следовательно можно составить уравнение: S=(B+11)*B.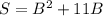 
Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение: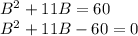
Далее решаем как обычное квадратное уравнение. В итоге получим что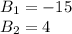 
. Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
А=15
и B=4.
Периметр будет равен (A+B)*2=(15+4)*2=19*2=38см.
Выразим катет а из формулы:
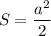
домножим обе части уравнения на два (и поменяем их местами заодно):
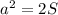
извлечём корень квадратный из обеих частей уравнения:
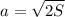
При площади треугольника в 10см², длина катета будет равна:
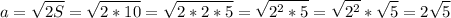см
Это точное значение (я его немного упростил, хотя можно было записать даже перемножив числа под корнем, получив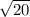 
)
Вычислим на калькуляторе это значение, получим десятичную дробь (с кучей знаков после запятой), затем округлим её до одного знака после запятой:
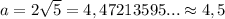см
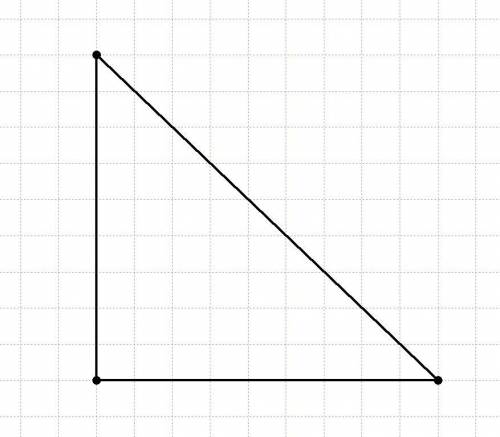
Начертить такой треугольник (используя приближённое значение длины катета) можно, расположив катеты по клеткам тетради (как раз будет ровное число клеток).
Равнобедренный прямоугольный треугольник выглядит как половинка квадрата с такой же стороной, как катет треугольника (смотри рисунок внизу).
2) = 8p- (6p²+16p-15p-40) = 8p-6p²-16p+15p+40 = - 6p²+7p+40
3)
a) 12x²+20х-3х-5=12х²-6х+42х-21
17х-5=36х-21
36х-17х=21-5
19х =16
х= 16/19 ответ: выражения равны при х=16/19
б) 10х-2-5х²+х = 2х-6-5х²+15х
11х-2-5х²=17х-6-5х²
11х-2=17х-6
17х-11х=6-2
6х=4
х=4/6 = 2/3
ответ: выражения равны при х =2/3