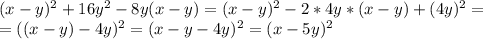
Для визначення, при якому значенні параметра "а" система не має рішень, ми можемо скористатися методом елімінації змінних. Спочатку помножимо перше рівняння на 5, щоб узгодити коефіцієнти при "у":
5*(х/2) + 5*(у/5) = 5*2
5x + y = 10
Тепер ми отримали систему рівнянь:
5x + y = 10
5x + 2y = a
Якщо відняти перше рівняння від другого, отримаємо:
(5x + 2y) - (5x + y) = a - 10
y = a - 10
Отже, умовою відсутності рішень є те, що після виконання вищенаведених кроків параметр "a" повинен мати таке значення, що "y" визначається виразом "a - 10". В іншому випадку, коли "a" приймає будь-яке інше значення, система матиме єдине рішення.

Объяснение:
Это дифференциальное уравнение с разделяющимися переменными, но одновременно это линейное однородное уравнение относительно функции (y-a). Недавно я показывал технику решения уравнений с разделяющимися переменными; повторяться мне не хотелось бы. Воспользуемся знаниями о линейных однородных уравнениях. Если уравнение имеет вид
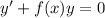
с непрерывной функцией f(x), то общее решение может быть найдено по формуле
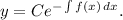
В нашем случае имеем следующее:
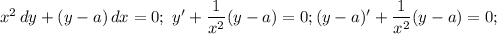
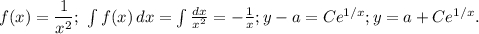
Замечание. При делении уравнения на x и dx было потеряно решение x=0 (при делении на dx можно было потерять решения x=c при любом c, но проверка показывает, что потеряно только решение x=0).