Войти
АнонимМатематика21 августа 15:52
Во сколько раз увеличится периметр квадрата и во сколько раз увеличится его площадь, если каждую сторону увеличить в
3 раза?
Соотношение параметров квадрата
Приведём формулы периметра Р и площади S квадрата через длину стороны а.
периметр квадрата Р равен учетверённому размеру его стороны а: Р = 4 * а;
площадь квадрата S равна квадрату его стороны а: S = a²;
периметр и площадь квадрата связаны между собой. так как в их формулах общий параметр - сторона квадрата: S = P² / 16.
Для понятного объяснения задачи увеличим по заданию его сторону в 3 раза.Тогда новая сторона квадрата станет а1 = 3 * а.
Вычисление увеличения периметра и площади квадрата
Чтобы узнать, как при этом изменились периметр и площадь квадрата, подставим в формулы Р и S вместо "а" новое значение стороны "а1". Тогда:
Р1 = 4 * а1 = 4 * (3 * а ) = 12 * а;
S1 = а1² = (3 * а)² = 9 * а².
После того, как выразили новый периметр Р1 и площадь S1 через начальное значение стороны "а", можно ответить на вопрос задания:
для вычислений используем написанные выше формулы для площади S и периметра P;
чтобы узнать, во сколько раз увеличится периметр квадрата, нужно разделить Р1 на Р;
чтобы узнать, во сколько раз увеличится площадь квадрата, нужно разделить S1 на S.
Согласно выше сказанного, ответим на вопросы задания:
во сколько раз увеличился периметр квадрата, для чего разделим (Р1 : Р) = (12 * а) : (4 * а) = 3 (раза);
во сколько раз увеличится площадь квадрата, для чего разделим (S1 : S) = (9 * а²) : (а²) = 9 (раз).
заметим, что если периметр квадрата увеличился в 3 раза, как и сторона квадрата, то площадь, увеличивается в (3)² = 9 раз.
ответ: периметр увеличится в 3 раза, площадь увеличится в 9 раз.
Объяснение:
1) найдем координаты вершины параболы по формуле
х₀=-b/2a
х₀=-6/(2(-1))=3
у₀=у(3)=-9+18-5=4
2) выразим х чрез у
y=-x²+6x-5
x²-6x+(y+5)=0 это квадратное уравнение решаем его по фрмуле корней
x₁₋₂=(-b±√d)/2a=(6±(√(36-4(у+5))))/2=(6±(√4(9-4(у+5))))/2=
=(6±2(√(9-(у+5))))/2=3±√(9-(у+5))=3±√(9-у-5)=3±√(4-у)
получилось 2 выражения
х=3+√(4-у)
х=3-√(4-у)
3) меняем местами х и у
y=3+√(4-x)
y=3-√(4-x)
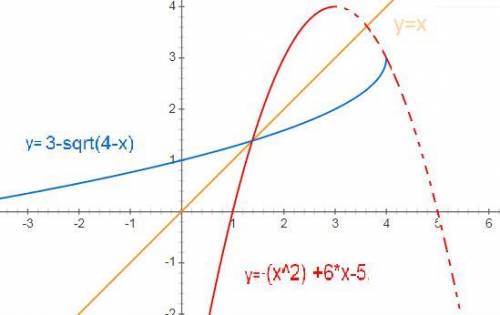
c учетом того, что графики прямой и обратной функции симметричны относительно прямой у=х
для х∈(-∞;3] обратной функцией будет y=3-√(4-x)
Дополнительно
график прямой и обратной функции
3x+5+8x+1=17
11x+6=17
11x=11
x=1