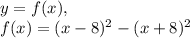
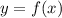 — прямая пропорциональность.
— прямая пропорциональность. — прямая пропорциональность, то есть доказать, что в выражении
— прямая пропорциональность, то есть доказать, что в выражении 
 находится в первой степени (не
находится в первой степени (не 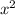 , не
, не 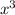 , не
, не 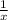 и не
и не 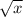 , а просто
, а просто  ).
). . Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид
. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид 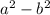 , где
, где 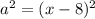 , и
, и 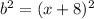 . Формула «разность квадратов» раскрывается так:
. Формула «разность квадратов» раскрывается так: 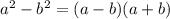 .
.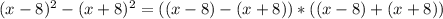
 .
.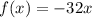 ,
,  находится в первой степени, а значит зависимость
находится в первой степени, а значит зависимость  — есть прямая пропорциональность. Доказано.
— есть прямая пропорциональность. Доказано.
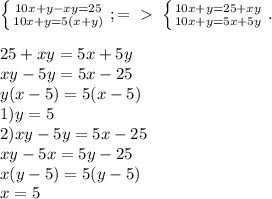
узнаем, сколько процентов участка может вспахать первая бригада за 1 час:
переведем часы в минуты - 1,5 ч = 90 мин и составим отношение:
90/30 = 60/x
90x = 1800
x = 20 %
узнаем, сколько процентов участка может вспахать вторая бригада за 1 час:
переведем часы в минуты - 2,1 ч = 126 мин и составим отношение:
126/70 = 60/x
126х = 4200
х = 33 % (примерно)
вместе за 1 час две бригады вспахивают около 53 % земли
20 % (первый час) + 53 % (второй час) + 27 % (около получаса) = 2,5 ч