(2+a)x^2+(1-a)x+a+5=0 Рассмотрим несколько ситуаций: 1)если старший коэффициент при x^2=0 ( при а=-2): 0*x^2+3x-2+5=0 3x+3=0 3x=-3 x=-1 Значит, a=-2 нам подходит 2) если средний коэффициент равен нулю ( при а=1): 3x^2+0*x+1+5=0 3x^2+6=0 3x^2=-6 - решений нет, значит а=1 нам не подходит. 3) если а не равно -2 и не равно 1, то перед нами квадратное уравнение, которое имеет хотя бы один корень тогда, когда дискриминант >=нуля: D= (1-a)^2-4(2+a)(a+5)>=0 1-2a+a^2-4(2a+10+a^2+5a)>=0 1-2a+a^2-4(a^2+7a+10)>=0 1-2a+a^2-4a^2-28a-40>=0 -3a^2-30a-39>=0 3a^2+30a+39<=0 | :3 a^2+10a+13<=0 a^2+10a+13=0 D=10^2-4*1*13=48 a1=(-10-4V3)/2=-5-2V3 a2=-5+2V3
Для упрощения сделаем в исходном тождестве замену x=63t и обозначим F(t)=R(63t). Т.к. R(x) - многочлен, то F(t) - тоже многочлен. Тогда, т.к. 2016=63*32, то исходное тождество перепишется в виде (t-32)F(t+1)=tF(t). Подставим в него t=0, получим -32F(1)=0*f(0), откуда F(1)=0. Подставим t=1, получим -31F(2)=F(1)=0, т.е. также F(2)=0. Затем подставляем последовательно t=2,3,...,31. Будем последовательно получать, F(3)=F(4)=...=F(32)=0. Если дальше подставить t=32, то получится опять 0=F(32). Дальнейшая подстановка t=33, не позволяет найти F(33), т.к. будет F(34)=33F(33). Аналогично, подстановкой t=-1, мы найдем -33F(0)=-F(-1), откуда не найти ни F(0) ни F(-1). Таким образом, пока установлено, что F(t) имеет корни 1,2,3,..., 32, а значит, он делится на (t-1)(t-2)·...·(t-32). Поэтому возникает предположение, что F(t) можно попробовать искать в виде F(t)=с(t-1)(t-2)·...·(t-32), где c - некоторая константа. Покажем, что этот F(t) действительно удовлетворяет тождеству: (t-32)F(t+1)=(t-32)·ct(t-1)·...·(t-31)=t·c(t-1)·...·(t-31)(t-32)=tF(t). Итак, некоторые F(t) найдены. Значит, в качестве R(x) можно взять, например R(x)=63³²F(x/63)=(x-63)(x-2·63)(x-3·63)·...·(x-32·63).
3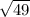 -2
-2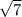 +
+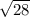 =3*7-2
=3*7-2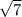 +
+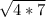 =21-2
=21-2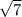 +2
+2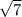 =21
=21