Объяснение:
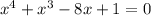
Выделим полную четвертую степень:
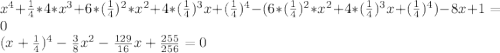
Сделаем замену: 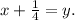
Откуда: 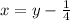
Уравнение примет вид:
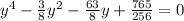
Домножим обе части уравнения на 256 и сделаем замену m = 4y;
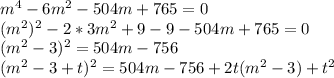 , где t - такое число, которое сворачивает правую часть в полный квадрат. Его следует найти, рассмотрев квадратный трехчлен относительно m и найдя его дискриминант и приравняв его к нулю:
, где t - такое число, которое сворачивает правую часть в полный квадрат. Его следует найти, рассмотрев квадратный трехчлен относительно m и найдя его дискриминант и приравняв его к нулю:
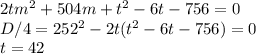 - корень. Значит, можно разделить данный трехчлен на (t - 42), получим:
- корень. Значит, можно разделить данный трехчлен на (t - 42), получим:
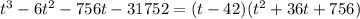
Очевидно, второй множитель не имеет действительных решений. Значит, t = 42. Напомню, что это такое число, при котором правая часть - полный квадрат. Подставим его.
^2 = (2\sqrt{21} (m+3))^2](/tpl/images/0545/9419/8a540.png)
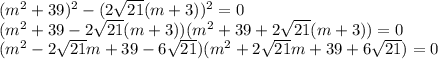
Рассмотрим первый множитель:
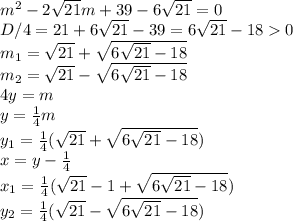
Аналогично рассмотрев второй множитель обнаружим, что D/4 < 0, а значит, действительных корней нет.
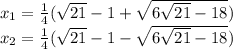
если решить как ваше уравнение то корень будет иррациональным так как по схеме горнера уже после 3 проверки идут корни очень плохие!
(5x)^(2x+1) = 5^(2x+1)*x^(2x+1) = 5*5^(2x)*x^(2x+1)
5*5^(2x)*x^(2x+1) + 5^(2x) = 5^(2x)*(5*x^(2x+1) + 1) = 750 = 6*5^3
Варианты:
{ 5^(2x) = 5^3, x = 3/2
{ 5*x^(2x+1) + 1 = 6, 5*x^(2x+1) = 5, x^(2x+1) = 1, (3/2)^4 = 1 - не подходит
{ 5^(2x) = 5^2, x = 1
{ 5*x^(2x+1) + 1 = 30, 5*x^(2x+1) = 29 - не подходит
{ 5^(2x) = 5, x = 1/2
{ 5*x^(2x+1) + 1 = 150, 5*x^(2x+1) = 149 - не подходит
{ 5^(2x) = 1, x = 0
{ 5*x^(2x+1) + 1 = 750, 5*x^(2x+1) = 749 - не подходит
может ошибка у вас там так как
(5)^(2x+1) +5^2x = 750
5^2x*5+5^2x=750
5^2x=t
6t=750
t=125
2x=3
x=3/2
теперь ставим
3/2^2+3/2 = 15/4
Область определения (или значения) функции - это ряд тех аргументов, при которых функция имеет смысл. Существует три случая в области определения определения функции:
1) если в правой части функции есть дробь, то знаменатель дроби не должен равняться нулю, в противном случае функция не имеет смысла : у=1/х - x \neq 0(в данном случае область определения функции от - бесконечности до +бесконечности, кроме нуля); y= 5/(x^2-1) - x^2-1 /neq 0 x^2 /neq 1 x /neq 1(область определения данной функции включает значения от - бесконечности до + бесконечности, исключая 1).
2) если функция имеет корень чётной степени, то значение под корнем не должно быть меньше нуля: y=корень из(х) - х>0, значит область определения функции составляет (0;+\infty).
3) если функция имеет и корень и дробь, тогда выражение под корнем не должно быть отрицательным, а выражение в знаменателе не должно равняться нулю: y=корень из(1/х+1), занчит, 1/х+1 > 0 х>-1 и х+1 /neq 0 x /neq -1(область определения этой функции содержит значения от -1 до плюс бесконечности).
У фукции y=x^2-4x+6 нет ни корней, ни дробей, поэтому область определения этой функции включает все значения числовой прямой.;)
Решение уравнения 4-ой степени методом Феррари.
Пусть имеется общий уравнения четвертной степени
В данном случае a = 1; b = 0; c = -8; d = 1.
Выполним замену, пусть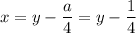 , получим
, получим
p = -3/8; q = -63/8; r = 765/256.
Подставляя коэффициенты в уравнение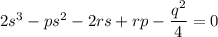
Мы получим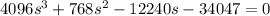 и решим это уравнение методом разложения на множителей
и решим это уравнение методом разложения на множителей
Получаем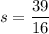
Это уравнение решений не имеет, так как D = -442368 < 0.
Далее подставляем коэффициент в квадратное уравнение вида
Выполнив обратную замену, получим ответ