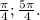Посмотри сначала, какое уравнение легче. Здесь 2 уравнение легче. 2х+у=10. Теперь берешь и выражаешь одно через другое, т.е. у=10-2х ← Получается, мы нашли у, подставляешь это значение (10-2х) вместо у ↑ в 1 уравнении, т.е. 5х - 3(10-2х) = 14 ↑ Далее обычно решаешь это уравнение ↑ 5х-30+6х=14 ↑ 11х=44 ↑ х=4. ↑ Ты уже нашла х, но ведь есть еще и у, его мы выразили чуть раньше ↑ Подставляешь в это выражение найденный х и все готово :) у=10-2х=10-2*4=10-8=2 ответ: (4;2) (ответ записываем в скобках, строго сначала х, потом у)
Парабола задаётся уравнением y = (x+a)² + b, где x - аргумент (числа, которые располагаются на оси Ox), a - смещение вершины параболы по оси Ox (если (x-1)² - смещение вправо, если (x+1)² - смещение влево относительно начала координат), b - смещение вершины параболы по оси Oy x²+1 - смещение на 1 вверх, x² - 1 - смещение на 1 вниз. График параболы имеет вид двух "изогнутых веточек", исходящих из вершины параболы и стремящихся вверх, если перед (x+a)² не стоит знака, вниз, если перед (x+a)² стоит минус, например: -(x+3)² + 6: график параболы смещён на 3 влево, на 6 вверх, а веточки параболы направлены вниз.
Гипербола задаётся уравнением y=1/(x+a) + b, где a,b - коэффициенты, также показывающие смещение по осям x,y аналогично предыдущему примеру.
Прямая задаётся уравнением y=kx+b, где k - коэффициент, показывающий, на сколько быстро возрастает функция (к примеру, если прямая задаётся как y=3x, то за один шаг по оси Ox наша прямая вырастет вверх на 3 таких же шага. А коэффициент b показывает то, в какой точке наша прямая пересекается с осью Oy.
а)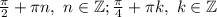 ; б)
; б) 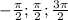 ;
; 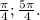
Объяснение:
Воспользуемся формулой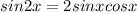
Выберем корни , принадлежащие отрезку![[-\frac{\pi }{2} ; \frac{3\pi }{2} ]](/tpl/images/0545/9591/789c4.png)
Из первой серии это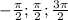
из второй