ответ: 21 см
Объяснение:
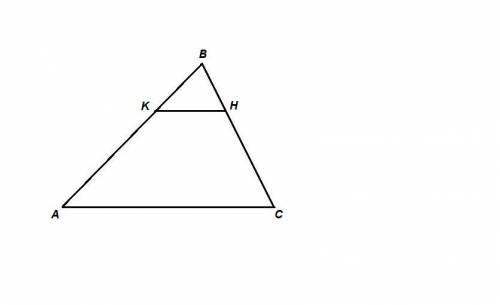
Дано: ΔАВС, КН║АС, Sakh : Sakhc = 1 : 8
Pakh = 7 см
Найти: Pabc.
Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sakh : Sakhc = 1 : 8, значит площадь треугольника АВС составляет 9 частей, тогда
Sakh : Sabc = 1 : 9 = k²
k = 1/3
Отношение периметром подобных треугольников равно коэффициенту подобия:
Pakh : Pabc = 1 : 3
Pabc = Pakh · 3 = 7 · 3 = 21 см
1) 3tg(п/2+п/4)+5sin(2П+П/2)-4*1/2=-3ctg(П/4)+5sin(П/2)-2=
=-3*1+5-2=0
2) -ctga*tga+cos^2a=cos^2a-1=cos^2a-cos^2a-sin^2a=-sin^2a
3) 2tg(2п-П/4)+7sin(4П+П/2)-8*1/2=-2tg(П/4)+7sin(П/2)-4=
=-2+7-4=1
4) -tgactga+sin^2a=sin^2a-1=-cos^2a