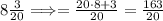
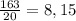
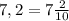
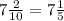
АКСИОМА НЕПРЕРЫВНОСТИ (ПРИНЦИП ДЕДЕКИНДА)
Пусть AA, BB -- непустые подмножества RR такие, что
∀a∈A,b∈B → a≤b.∀a∈A,b∈B → a≤b.
Тогда существует c∈Rc∈R такое, что
∀a∈A,b∈B → a≤c≤b.
НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ АКСИОМ МНОЖЕСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Число 0 единственно.
Для любого aa число (−a)(−a), противоположное к aa единственно.
Для любых a,b∈Ra,b∈R существует единственное xx такое, что a+x=ba+x=b (при этом x=b+(−a)x=b+(−a); это число называется разностью между bb и aa и обозначается b−ab−a).
Число 1 единственно.
а)х^3-9x=x(x^2-9)=x(x-3)(x+3)
б)-5а^2-10ab-5b^2=5a^2+10ab+5b^2=5(a^2+2ab+b^2)=5(a+b)^2