Решить уравнение 6x^4-3x^3+12x^2-6x=0

Question

Алгебра: Решить уравнение 6x^4-3x^3+12x^2-6x=0

Torisan · Accepted Answer

1) проверяем условие при наименьшем возможном значении n.

n>5, значит проверяем условие при n=6

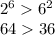
$2^66^2 \\ 6436$

Верно!

2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:

2^kk^2

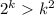
3) Тогда при n=k+1 должно выполняться неравенство:

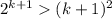
$2^{k+1}(k+1)^2$

Вернемся к неравенству из второго пункта и домножим его на 2:

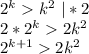
$2^kk^2 \ |*2 \\ 2*2^k2k^2 \\ 2^{k+1}2k^2$

Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:

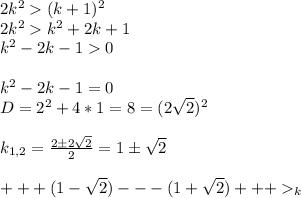
$2k^2(k+1)^2 \\ 2k^2k^2+2k+1 \\ k^2-2k-10 \\ \\ k^2-2k-1=0 \\ D=2^2+4*1=8=(2\sqrt{2})^2 \\ \\ k_{1,2}=\frac{2 \pm2\sqrt{2}}{2}=1 \pm \sqrt{2} \\ \\ +++(1-\sqrt{2})---(1+\sqrt{2})+++_k$

по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)

Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5

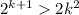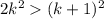Если $2^{k+1}2k^2$ , а 2k^2(k+1)^2 , при k>5

То есть, 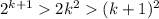$2^{k+1}2k^2(k+1)^2$ , при k>5, то по закону транзитивности:

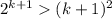$2^{k+1}(k+1)^2$ , при k>5 - ч.т.д

MOGZ ответил