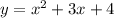
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
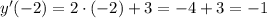
Уравнение касательной имеет вид:
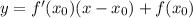
Подставим значение 
Итак, уравнение касательной заданной функции: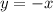 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
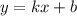численно равен тангенсу угла наклона 
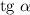с положительным направлением оси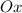 
В найденной касательной коэффициент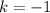 
, следовательно, 
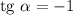при 
или 
ответ: или
За интеграл я буду Июиспользовать вот этот знак:
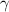
1) Перепишите дробь:
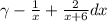
2) Использовать свойства интегралов:
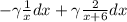
3) Вычислить интегралы и прибавить константу интегрирования С:
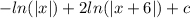
1) Найти неопределённый интеграл:
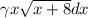
2) Упростить интеграл, используя метод замены переменной:
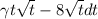
3) Преобразовать выражения:
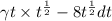
4) Вычислить произведение:
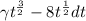
5) Использовать свойство интегралов:
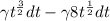
6) Вычислить интегралы:
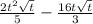
7) Выполнить обратную замену:
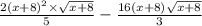
8) Упростить выражение:
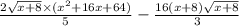
9) Вернуть пределы интегрирования и подставить в пример (8):
V = S'(3) = 4 × 3 - 2 = 10
Eк = (mV²)/2 = (5 × 10²)/2 = 250 Дж