Решить уравнения 1) x^2 - 4x + 4 =0 2) x^2 - 6x + 9 =0 3) (5-2x)^2 - 1 = x(4x + 2) 4) (2x - 3)^2 + 2 = 4x(x - 1)

👇

Ответ:

nikitaviktorov9

10.10.2021

1) (x-2)^2 => x = 2
Или же за теоремой Виета: x1=2 x2=2
2)За теоремой Виэта:
X1=3 x2=3
3)25-20x+4x^2-1=4x^2+2x
22x=24
x = 24/22 = 1 и 2/22
4)4x^2-12x+9+2=4x^2-4x
-8x=-11
x=11/8= 1 и 3/8 = 1,375

4,5(36 оценок)

Открыть все ответы

Ответ:

Dimaaaaaaasiiiiiik

10.10.2021

Объяснение:

Ограничения:

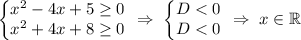
$\left\{\begin{matrix} x^2-4x+5\geq 0\\ x^2+4x+8\geq 0 \end{matrix}\right. \ \Rightarrow \ \left\{\begin{matrix} D$

$(4x-8)\sqrt{x^2-4x+5}-(x+2)\sqrt{x^2+4x+8}+x-6=0 \\ \\ 4(x-2)\sqrt{x^2-4x+5}-(x+2)\sqrt{x^2+4x+8}+x-6=0 \ |:4 \\ \\ (x-2)\sqrt{x^2-4x+5}-\frac{x+2}{2}\frac{\sqrt{x^2+4x+4+4}}{2}+\frac{x-6}{4}=0 \\ \\ (x-2)\sqrt{x^2-4x+4+1}-\frac{x+2}{2}\sqrt{\frac{(x+2)^2+4}{4}}+\frac{x-6}{4}=0 \\ \\ (x-2)\sqrt{(x-2)^2+1}-\frac{x+2}{2}\sqrt{\left(\frac{x+2}{2}\right)^2+1}+\frac{x-6}{4}=0$

Замечаем, что первые два слагаемых имеют общую структуру в виде функции:

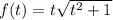
$f(t)=t\sqrt{t^2+1}$

Действительно, если вместо t подставить x-2, то

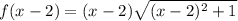
$f(x-2)=(x-2)\sqrt{(x-2)^2+1}$

Аналогично

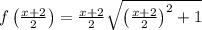
$f\left(\frac{x+2}{2}\right)= \frac{x+2}{2}\sqrt{\left(\frac{x+2}{2}\right)^2+1}$

Тогда 3-е слагаемое нашего уравнения представим в виде разности двух линейных функций вида: g(t)=at

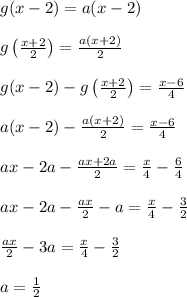
$g(x-2)=a(x-2)\\ \\g\left(\frac{x+2}{2}\right)= \frac{a(x+2)}{2} \\ \\ g(x-2)-g\left(\frac{x+2}{2}\right)=\frac{x-6}{4} \\ \\ a(x-2)- \frac{a(x+2)}{2}=\frac{x-6}{4} \\ \\ ax-2a-\frac{ax+2a}{2} =\frac{x}{4} -\frac{6}{4} \\ \\ ax-2a-\frac{ax}{2}-a=\frac{x}{4} -\frac{3}{2} \\ \\ \frac{ax}{2} -3a=\frac{x}{4}-\frac{3}{2} \\ \\ a=\frac{1}{2}$

Дополним g(t) к основной функции:

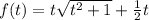
$f(t)=t\sqrt{t^2+1}+\frac{1}{2}t$

Исследуем ее на монотонность с производной

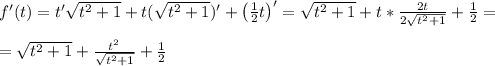
$f'(t)=t'\sqrt{t^2+1}+t(\sqrt{t^2+1})'+\left(\frac{1}{2}t\right)'=\sqrt{t^2+1}+t*\frac{2t}{2\sqrt{t^2+1}} +\frac{1}{2} =\\ \\=\sqrt{t^2+1}+\frac{t^2}{\sqrt{t^2+1}} +\frac{1}{2}$

Заметим, что t²≥0; √(t²+1)>0, при любых действительных t, тогда

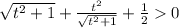
$\sqrt{t^2+1}+\frac{t^2}{\sqrt{t^2+1}} +\frac{1}{2}0$

Значит f'(t)>0, следовательно f(t) - монотонно возрастающая функция на всей числовой оси

Для монотонных функций справедливо:

f(a)=f(b) ⇔ a=b

Перепишем наше уравнение в следующем виде

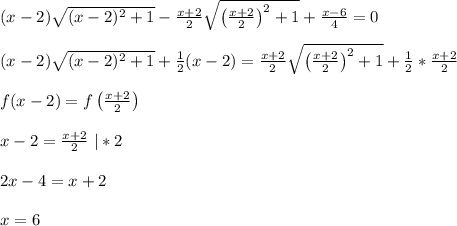
$(x-2)\sqrt{(x-2)^2+1}-\frac{x+2}{2}\sqrt{\left(\frac{x+2}{2}\right)^2+1}+\frac{x-6}{4}=0 \\ \\ (x-2)\sqrt{(x-2)^2+1}+\frac{1}{2}(x-2)=\frac{x+2}{2}\sqrt{\left(\frac{x+2}{2}\right)^2+1}+\frac{1}{2}* \frac{x+2}{2} \\ \\ f(x-2)=f\left(\frac{x+2}{2}\right) \\ \\ x-2=\frac{x+2}{2} \ |*2 \\ \\ 2x-4=x+2 \\ \\ x=6$