Считать будем все броски подряд, из которых нечетные (1, 3, 5) делает первый игрок, а четные (2, 4, 6) - второй.
Первый побеждает в следующих ситуациях:
- попал 1 броском
- попал 3 броском, а все предыдущие броски закончились промахом
- попал 5 броском, а все предыдущие броски закончились промахом
Второй побеждает в следующих ситуациях:
- попал 2 броском, а предыдущий бросок закончился промахом
- попал 4 броском, а все предыдущие броски закончились промахом
- попал 6 броском, а все предыдущие броски закончились промахом
Зная вероятность попадания 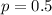 , вычислим вероятность промаха:
, вычислим вероятность промаха:
 :
:
Вероятность победы первого игрока:
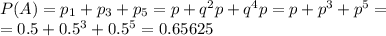
Вероятность победы второго игрока:
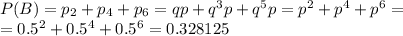
ответ: победа первого с вероятностью 0.65625, победа второго с вероятностью 0.328125