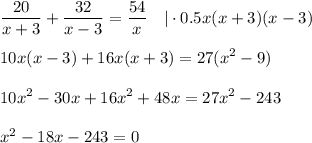
не удовлетворяет условию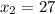
км/ч - собственная скорость
Дано: треугольник ABC. AB = 6, BC = 8, AC = 10;
M,N, K - соответственно середины сторон AB, BC, AC.
Найти: Периметр MNK (Pmnk) - ?
Решение: 1) В треугольнике ABC MN проходит через середины AB и BC, а значит по свойству средней линии треугольника параллельна и равна одной второй стороны AC. Соответственно, NK и MK составляют одну вторую от сторон AB и BC. Значит, все стороны треугольника MNK в два раза меньше сторон треугольника ABC.
MN = 5; NK = 3; MK = 4. P такого треугольника равен = 5+3+4 = 12. Ну и всё. )
1) p^12 :p^2 =p^(12-2) =p^10
2) a^16 :a^7 =a^(16-7) =a^9
3) 10^21 :10^12 =10^(21-12) =10^9
4) y^9 :y =y^(9-1) =y^8
5) 2.3^17 :2.3^8 =2.3^(17-8) =2.3^9
6) q^12 :q^8 =q^(12-8) =q^4
при умножении степени складываются
1) a^3 *a^4 =a^(3+4) =a^7
2) a*a^5 =a^(1+5) =a^6
3) x^5 *x^3 =x^8
4) 0.5^3 *0.5^7 =0.5^10
5) p^2 *p^3 =p^5
6) q^4 *q^5 =q^9
7) y^3 *y^5 =y^8