График построен
Объяснение:
y = -x² + 2x + 8 - это парабола, ветви которой направлены вниз (a < 0).
Найдём вершину:
x = - 2 / (2 * (-1)) = 1
y = -1² + 2*1 + 8 = -1 + 2 + 8 = 9
Итак, вершина: (1; 9).
По т-ме Виета корни уравнения x² + 2x + 8: x₁ = -2, x₂ = 4. Эти точки - точки пересечения графика с осью ОХ.
С вершины т.(1; 9) проводим ветви вниз, которые пересекут ось ОХ в точках (-2; 0) и (4; 0).
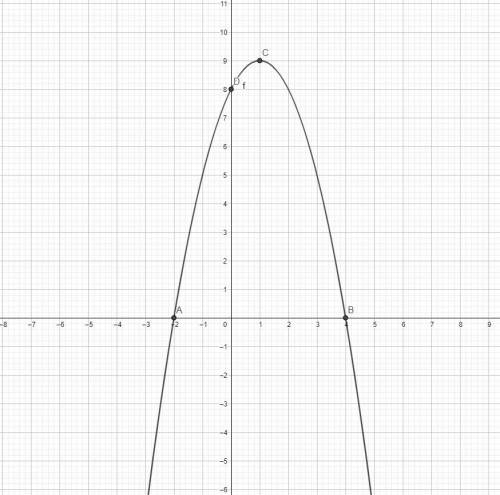
На фото:
т. С(1; 9) - вершина;
т. D(0; 8) - точка пересечения графика с осью ОY;
т. А(-2; 0) и т.В(4; 0) - точки пересечения графика с осью ОХ.
№ 2:
при каком значении параметра a уравнение |x^2−2x−3|=a имеет три корня?
введем функцию
y=|x^2−2x−3|
рассмотрим функцию без модуля
y=x^2−2x−3
y=(x−3)(х+1)
при х=3 и х=-1 - у=0
х вершины = 2/2=1
у вершины = 1-2-3=-4
после применения модуля график отражается в верхнюю полуплоскость
при а=0 - 2 корня (нули х=3 и х=-1)
при 0< а< 4 - 4 корня (2 от исходной параболы, 2 от отображенной части)
при а=4 - 3 корня (2 от исходной параболы, 1 от вершины х=1)
при а> 4 - 2 корня (от исходной параболы)
ответ: 4
√(3-4y) имеет смысл выражение при (3-4y)≥0 ⇔y≤3/4 или y≤0,75