Первое задание
Число делится на 4, если число, составленное из последних двух цифр, делится на 4. В данном случае это 37628 (ведь 28 делится на 4).
ответ: 37628.
Второе задание
Преобразуем это число по правилам действий со степенями:
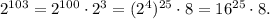
Число 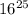 оканчивается на 6, потому что любое число, оканчивающееся на 6, в любой степени тоже оканчивается на 6. Затем, если мы умножим это число на 8, то получим число, оканчивающееся на 8 (потому что
оканчивается на 6, потому что любое число, оканчивающееся на 6, в любой степени тоже оканчивается на 6. Затем, если мы умножим это число на 8, то получим число, оканчивающееся на 8 (потому что 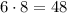 ).
).
ответ: на 8.
Третье задание
Преобразуем выражение по правилам действий со степенями:
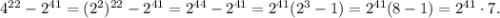
ответ: на 7.
***
Если будут какие-нибудь вопросы — задавайте.
Если мой ответ оказался полезен, отмечайте его как «лучший ответ».
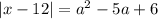
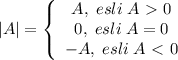
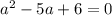 при
при 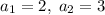 .
.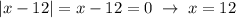 .
.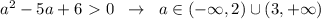
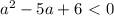 , то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае
, то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае 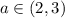 .
.
(b-1/5)(b²+b/5+1/25)
(1/3-t)(1/9+t/3+t²)