Решение системы уравнений а=3
у=0
Объяснение:
(у+1)/(2а-4)=1/2
(5а+у)/(3а+6)=1
(у+1)/(2а-4)=0,5
(5а+у)/(3а+6)=1
Умножить знаменатели дробей на левую часть, чтобы избавиться от дробного выражения:
у+1=0,5(2а-4)
5а+у=3а+6
у+1=а-2
5а+у=3а+6
Перенесём неизвестные в левую часть уравнений, известные в правую:
у-а= -3
2а+у=6
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно первое уравнение умножить на -1:
-у+а=3
2а+у=6
Складываем уравнения:
-у+у+а+2а=3+6
3а=9
а=3
Теперь значение а подставляем в любое из двух уравнений системы и вычисляем у:
у-а= -3
у= -3+а
у= -3+3
у=0
Решение системы уравнений а=3
у=0
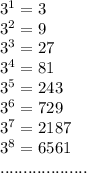
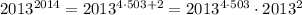
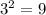, то есть 9.
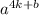заканчивается на такую же цифру, как и число 
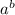. Аналогично,
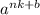оканчивается на такую же цифру, что и число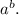 
Скорость автомобиля - (х+15) км/ч
Скорость сближения - (х+х+15) км/ч
Время в пути - 2 1/3 часа
Расстояние - 245 км
Уравнение.
2 1/3 × (х+х+15) = 245
7/3 × (2х +15 ) =245
2х+15 = 245 ÷ 7/3
2х+15 = 245/1 × 3/7
2х+15= 105
2х=105-15
2х=90
х=90/2
х=45 км/ час - скорость автобуса
45 +15 = 60 км/ч - скорость автомобиля
Проверим:
2 1/3 × (45+60) = 7/3 × 105/1 = 7×35 = 245 км - расстояние
ответ: 45 км/ч скорость автобуса , 60 км/час скорость автомобиля.