Дана функція:
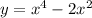
Знайдемо її похідну ( y' = g(x) ):
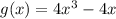
Знайдемо значення похідної в 0 (g(x) = 0):
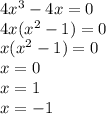
Ми знайшли 3 можливі точки екстремуму: 0, 1, -1. Перевіримо, чи дійсно ці точки є екстремумами функції:
1) Підставимо в похідну точку -2. Значення від'ємне, отже функція спадає;
2) Підставимо в похідну точку -0.5. Значення додатне, отже функція зростає;
3) Підставимо в похідну точку 0.5. Значення від'ємне, отже функція спадає;
4) Підставимо в похідну точку 2. Значення додатне, отже функція зростає.
Отже на проміжку xє(-∞;-1) функція спадає; хє(-1;0) – функція зростає; хє(0;1) – функція спадає; хє(1;+∞) – функція зростає. Отже ці точки дійсно є екстремумами функції.
Відповідь: -1, 0, 1.
через данную точку, мы должны, взять значение икса в данной точке, и подставить данное значение в функцию:
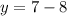
5ˇ(x)-5ˇx.5ˇ(-2)=120
5ˇ(x).(1-1/25)=120
24/25 . 5ˇ(x)=120
5ˇ(x)=120.25/24
5ˇ(x)=5.25
5ˇ(x)=5ˇ(3)
x=3
2)4ˇ(x)-4ˇ(x-2)=60
4ˇ(x)-4ˇ(x).4ˇ(-2)=60
4ˇ(x)(1-1/16)=60
4ˇ(x). 15/16=60
4ˇ(x)=60.16/15
4ˇ(x)=4.16
4ˇ(x)=4ˇ(3)
x=3